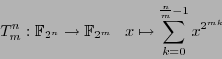


Siguiente: Bibliography
Arriba: Algorithms for field arithmetic
Anterior: Square root
If 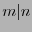 then
then
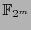 is a subfield of
is a subfield of
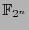 , or
, or
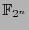 is an extension of
is an extension of
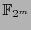 . In this case, the map
. In this case, the map
is called the trace. 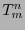 is a
is a
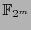 -linear map. Consequently,
-linear map. Consequently,
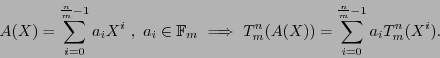 |
(11) |
And,
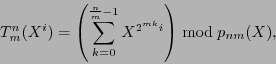 |
(12) |
where
![$p_{nm}(X)\in\mathbb{F}_m[X]$](img141.png) is an irreducible polynomial of degree
is an irreducible polynomial of degree 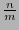 . Then by pre-computing the values at (12), the values of the trace can be calculated according to relation (11).
. Then by pre-computing the values at (12), the values of the trace can be calculated according to relation (11).
Guillermo M. Luna
2010-02-19
![]() then
then
![]() is a subfield of
is a subfield of
![]() , or
, or
![]() is an extension of
is an extension of
![]() . In this case, the map
. In this case, the map