


Siguiente: Trace
Arriba: Algorithms for field arithmetic
Anterior: Squaring
Since
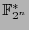 is a cyclic group of order
is a cyclic group of order  we have that for all
we have that for all
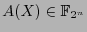 :
:
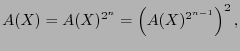 thus
thus
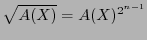 , and being squaring a linear map:
, and being squaring a linear map:
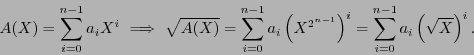 |
(8) |
If 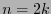 is an even number,
is an even number,
If 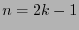 is an odd number,
is an odd number,
and clearly,
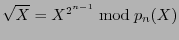 .
.
Guillermo M. Luna
2010-02-19
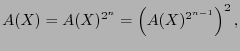 thus
thus
![]() is a cyclic group of order
is a cyclic group of order ![]() we have that for all
we have that for all
![]() :
:
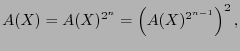 thus
thus
![]() , and being squaring a linear map:
, and being squaring a linear map: