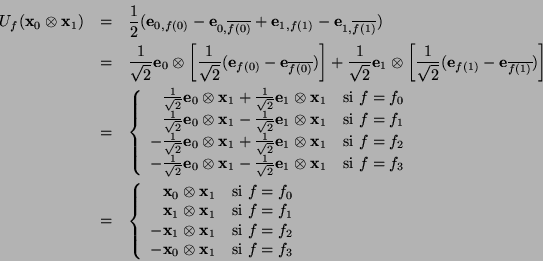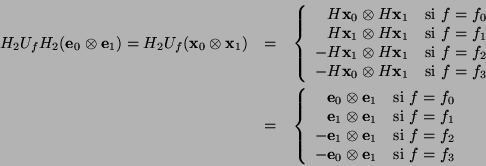


Posterior: Algoritmo para el cálculo
Arriba: Nociones básicas de Computación
Anterior: Evaluación de funciones booleanas
Sea 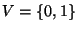 el conjunto de valores de verdad clásicos. De las
el conjunto de valores de verdad clásicos. De las 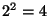 funciones booleanas
funciones booleanas 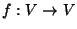 dos son constantes y las otras dos son equilibradas. Al nombrarlas
dos son constantes y las otras dos son equilibradas. Al nombrarlas
se tiene que las funciones constantes son 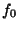 y
y 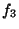 , y las equilibradas son
, y las equilibradas son 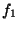 y
y 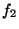 .
.
El propósito del algoritmo de Deutsch-Jozsa es decidir, para una 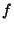 dada, si acaso es constante o equilibrada ``utilizando un solo paso de cómputo''.
dada, si acaso es constante o equilibrada ``utilizando un solo paso de cómputo''.
Sea 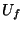 una matriz permutación de orden
una matriz permutación de orden
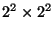 tal que
tal que
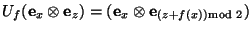 .
. 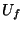 es pues unitaria. De hecho es muy similar al funcionamiento de la compuerta ``negación controlada'', salvo que en aquella, la función
es pues unitaria. De hecho es muy similar al funcionamiento de la compuerta ``negación controlada'', salvo que en aquella, la función 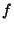 es propiamente la identidad. En la tabla 1 ilustramos la acción de
es propiamente la identidad. En la tabla 1 ilustramos la acción de 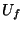 refiriéndonos solamente a los índices de vectores básicos.
refiriéndonos solamente a los índices de vectores básicos.
Recuadro 1:
Acción de la matriz unitaria 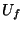 en el algoritmo de Deutsch-Jozsa.
en el algoritmo de Deutsch-Jozsa.
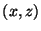 |
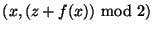 |
| (0,0) |
(0,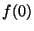 ) ) |
| (0,1) |
(0,
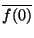 ) ) |
| (1,0) |
(1,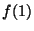 ) ) |
| (1,1) |
(1,
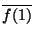 ) ) |
|
Considerando el operador de Hadamard 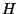 , hagamos
, hagamos
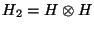 .
Primero se tiene,
.
Primero se tiene,
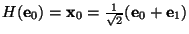 y
y
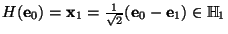 y luego
y luego
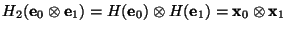 . Claramente,
. Claramente,
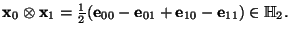 Por tanto,
Por tanto,
En consecuencia,
vale decir, al aplicar el algoritmo cuántico 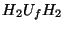 (nótese que utilizamos notación algebraica: los operadores se aplican de derecha a izquierda), partiendo del vector básico
(nótese que utilizamos notación algebraica: los operadores se aplican de derecha a izquierda), partiendo del vector básico
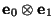 se obtiene un vector de la forma
se obtiene un vector de la forma
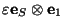 donde
donde
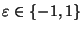 es un signo y
es un signo y 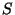 es una señal que indica si acaso
es una señal que indica si acaso 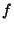 es o no equilibrada. En otras palabras, la respuesta
es o no equilibrada. En otras palabras, la respuesta 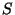 coincide con
coincide con
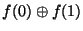 , donde
, donde 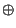 es la disyunción excluyente, XOR. La auscultación del valor
es la disyunción excluyente, XOR. La auscultación del valor 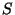 se realiza siguiendo el postulado de medición, y su valor está apareciendo leyendo sólo el primer qubit. Al efectuar la medición se elige al vector básico
se realiza siguiendo el postulado de medición, y su valor está apareciendo leyendo sólo el primer qubit. Al efectuar la medición se elige al vector básico
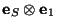 con probabilidad
con probabilidad
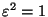 .
.



Posterior: Algoritmo para el cálculo
Arriba: Nociones básicas de Computación
Anterior: Evaluación de funciones booleanas
Guillermo Morales-Luna gmorales at cs.cinvestav.mx
2003-12-11
![]() el conjunto de valores de verdad clásicos. De las
el conjunto de valores de verdad clásicos. De las ![]() funciones booleanas
funciones booleanas ![]() dos son constantes y las otras dos son equilibradas. Al nombrarlas
dos son constantes y las otras dos son equilibradas. Al nombrarlas
![]() dada, si acaso es constante o equilibrada ``utilizando un solo paso de cómputo''.
dada, si acaso es constante o equilibrada ``utilizando un solo paso de cómputo''.
![]() una matriz permutación de orden
una matriz permutación de orden
![]() tal que
tal que
![]() .
. ![]() es pues unitaria. De hecho es muy similar al funcionamiento de la compuerta ``negación controlada'', salvo que en aquella, la función
es pues unitaria. De hecho es muy similar al funcionamiento de la compuerta ``negación controlada'', salvo que en aquella, la función ![]() es propiamente la identidad. En la tabla 1 ilustramos la acción de
es propiamente la identidad. En la tabla 1 ilustramos la acción de ![]() refiriéndonos solamente a los índices de vectores básicos.
refiriéndonos solamente a los índices de vectores básicos.
![]() , hagamos
, hagamos
![]() .
Primero se tiene,
.
Primero se tiene,
![]() y
y
![]() y luego
y luego
![]() . Claramente,
. Claramente,
![]() Por tanto,
Por tanto,