Posterior: Algoritmo de Shor Arriba: Un poco de computación Anterior: Algoritmo de Deutsch-Jozsa

Algoritmo para el cálculo de la Transformada Discreta de Fourier

Sea $f:[\![0,n-1]\!]\to \mathbb{C}$ una función. La transformada discreta de Fourier de $f$ es la función $\hat{f}:[\![0,n-1]\!]\to \mathbb{C}$ tal que para cada $j\in [\![0,n-1]\!]$: $\hat{f}(j) = \frac{1}{\sqrt{n}}\sum_{k=0}^{n-1}\mbox{exp}\left(\frac{2\pi i j k}{n}\right) f(k)$. Aquí $i$ es la raíz cuadrada de -1.

En $\mathbb{C}^n$ consideremos la base canónica formada por los vectores $\mbox{\bf e}_j=\left(\delta_{ij}\right)_{i=0}^{n-1}$, $j=0,\ldots,n-1$. Para cada vector $\mbox{\bf f}=\sum_{j=0}^{n-1} f(j)\mbox{\bf e}_j\in\mathbb{C}^n$, su transformada discreta de Fourier es $\mbox{TDF}(\mbox{\bf f})=\hat{\mbox{\bf f}}=\sum_{j=0}^{n-1} \hat{f}(j)\mbox{\bf e}_j\in\mathbb{C}^n$. Es claro que $\mbox{TDF}$ es una transformación lineal y, respecto a la base canónica de $\mathbb{C}^n$, se representa por la matriz $\mbox{TDF}=\frac{1}{\sqrt{n}}\left(\mbox{exp}\left(\frac{2\pi i j k}{n}\right)\right)_{jk}$, la cual es en efecto unitaria, de hecho la matriz hermitiana de $\mbox{TDF}$, $\mbox{TDF}^H$, tiene la misma estructura que $\mbox{TDF}$ salvo que los exponentes en cada entrada tienen el signo ``$-$''.

En particular, se tiene

$$\forall j\in [\![0,n-1]\!]:\ \mbox{TDF}(\mbox{\bf e}_j)=\fra... ...n-1}\mbox{exp}\left(\frac{2\pi i j k}{n}\right)\mbox{\bf e}_k.$$ (6)

y, por supuesto,

$$\mbox{TDF}(\mbox{\bf f})=\sum_{j=0}^{n-1}f(j)\, \mbox{TDF}(\mbox{\bf e}_j).$$ (7)

Ahora, supongamos que $n=2^{\nu}$ es una potencia de 2. En este caso, la $\mbox{TDF}$ puede calcularse mediante el procedimiento de la llamada transformada rápida de Fourier $\mbox{TRF}$ (o si se quiere, $\mbox{FFT}$ por sus siglas en inglés: Fast Fourier Transform). Este procedimiento es de complejidad en tiempo $O(\nu 2^{\nu})= O(n\log n)$. Mas utilizando el paralelismo inherente a la computación cuántica, se le calculará aquí en un tiempo $O(\nu)$.

Observamos, por un lado, que $\mathbb{H}_{\nu} = \mathbb{C}^n$, y por otro lado, de la ecuación (6), que para los primeros valores de $\nu$ se tiene:

$\nu=1$

$$\begin{eqnarray*} \mbox{TDF}(\mbox{\bf e}_{0}) &=& \frac{1}{\sqrt{2}}(\mbox{\bf ... ... &=& \frac{1}{\sqrt{2}}(\mbox{\bf e}_{0}-\mbox{\bf e}_{1}) %%\\ \end{eqnarray*}$$

$\nu=2$

$$\begin{eqnarray*} \mbox{TDF}(\mbox{\bf e}_{00}) &=& \frac{1}{\sqrt{2}}(\mbox{\bf... ...mes \frac{1}{\sqrt{2}}(\mbox{\bf e}_{0}-i\mbox{\bf e}_{1}) %%\\ \end{eqnarray*}$$

De manera general, a cada índice $j\in[\![0,2^{\nu}-1]\!]$ lo identificaremos con la palabra $\mbox{\boldmath$\varepsilon$}_j = \varepsilon_{j,\nu-1}\cdots \varepsilon_{j,1}\varepsilon_{j,0}$ que lo representa en base 2. Así, el vector básico $\mbox{\bf e}_{\mbox{\scriptsize\boldmath$\varepsilon$}_j}\in\mathbb{H}_{\nu}$ es el producto tensorial de los vectores básicos $\mbox{\bf e}_{\varepsilon_{j,k}}\in\mathbb{H}_{1}$. Tendremos entonces, en $\mathbb{H}_{\nu}$, que para cada $j=0,\ldots, 2^{\nu}-1$:

$$\mbox{TDF}(\mbox{\bf e}_{\mbox{\scriptsize\boldmath$\varepsilon$}_j}) = \bigotimes_{k=0}^{\nu-1} \frac{1}{\sqrt{2}}\left(\mbox{\bf e}_{0}+\mbox{exp}\left(\frac{\pi i j}{2^{k}}\right)\mbox{\bf e}_{1}\right)$$

$$= {\scriptstyle \frac{1}{\sqrt{2}}\left(\mbox{\scriptsize\bf e}_{0}... ... exp}\left(\frac{\pi i j}{2^{\nu-1}}\right)\mbox{\scriptsize\bf e}_{1}\right) }$$ (8)

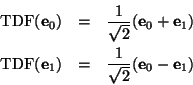
La forma de los factores en este producto tensorial sugiere considerar los operadores $Q_k:\mathbb{H}_1\to\mathbb{H}_1$ con representación, respecto a la base canónica, dada mediante la matriz unitaria $Q_k = \left[\begin{array}{cl} 1 & 0 \\ 0 & \mbox{exp}\left(\frac{\pi i}{2^{k}}\right) \end{array}\right]$. De hecho, como en (8) la potencia en la exponenciación va cambiando, podemos considerar más bien un correspondiente operador ``controlado'': $Q^c_{kj} = \left[\begin{array}{cl} 1 & 0 \\ 0 & \mbox{exp}\left(\pi i\frac{j}{2^{k}}\right) \end{array}\right]$. Así, por ejemplo, si $j=1$ entonces $Q^c_{k1} =Q_k$ en tanto que si $j=0$ entonces $Q^c_{k0} = I$ coincide con la identidad.

Observamos además que para $\mbox{\bf x}_0=\frac{1}{\sqrt{2}}(\mbox{\bf e}_0+\mbox{\bf e}_1)=H(\mbox{\bf e}_0)$ se tiene $Q^c_{kj}(\mbox{\bf x}_0) = \frac{1}{\sqrt{2}}\left(\mbox{\bf e}_{0}+\mbox{exp}\left(\pi i\frac{j}{2^{k}}\right)\mbox{\bf e}_{1}\right)$.

Ahora, a cada $j\in[\![0,2^{\nu}-1]\!]$ representémoslo en base-2 mediante la palabra $\mbox{\boldmath$\varepsilon$}_j$. Se tiene que para cada $\ell\in[\![0,\nu-1]\!]$, $\frac{\varepsilon_{j,\ell} 2^{\ell}}{2^{k}} = \frac{\varepsilon_{j,\ell}}{2^{k-\ell}}$. Por tanto, $\mbox{exp}\left(\pi i\frac{j}{2^{k}}\right) = \mbox{exp}\left(\pi i\frac{\sum_{... ...l=0}^{\nu-1}\mbox{exp}\left(\pi i\frac{\varepsilon_{j,\ell}}{2^{k-\ell}}\right)$ y en consecuencia, $Q^c_{kj} = Q^c_{k-\nu+1,\varepsilon_{j,\nu-1}}\circ \cdots \circ Q^c_{k-1,\varepsilon_{j,1}}\circ Q^c_{k,\varepsilon_{j,0}}$. Como $k$ ha de variar entre 0 y $\nu-1$ vemos que se ha de disponer de $2(2\nu-1)$ compuertas de la forma $Q^c_{\kappa\varepsilon}$, $\kappa\in[\![-(\nu-1),\nu-1]\!]$, $\varepsilon\in\{0,1\}$.

Observamos también que si $j<2^{\nu_1}$, con $\nu_1\leq \nu$ entonces todos los dígitos, en su representación binaria, con índices entre $\nu_1-1$ y $\nu-1$ son 0, y por tanto las correspondientes compuertas controladas actuarán como la identidad. Definamos pues para cada $(j,k)\in [\![0,2^{\nu}-1]\!] \times [\![0,\nu-1]\!]$,

$$P_{jk} = Q^c_{k-\nu_1+1,\varepsilon_{j,\nu_1-1}}\circ \cdots... ...rc Q^c_{k-1,\varepsilon_{j,1}}\circ Q^c_{k,\varepsilon_{j,0}},$$ (9)

donde $\nu_1=\lceil\log_2 j\rceil +1$. Tenemos pues: $P_{jk}(\mbox{\bf x}_0) = \frac{1}{\sqrt{2}}\left(\mbox{\bf e}_{0}+\mbox{exp}\left(\pi i\frac{j}{2^{k}}\right)\mbox{\bf e}_{1}\right)$.

Fijo $j\in[\![0,2^{\nu}-1]\!]$ para $k=0,\ldots,\nu-1$ los términos $P_{jk}(\mbox{\bf x}_0)$ van dando los de la derecha de la ec. (8) y éstos van apareciendo de izquierda a derecha según se les muestra ahí. Sin embargo, para cada $k\in[\![0,\nu-1]\!]$ observamos que en la definición (9) se está utilizando una notación algebraica, es decir, los operadores $Q^c_{k-\ell,\varepsilon_{j,\ell}}$ se aplican en orden inverso: de derecha a izquierda. De hecho, haciendo un poco más explícita la definición (9) se tiene:

$$\begin{eqnarray*} Q^c_{0,\varepsilon_{j,0}}(\mbox{\bf x}_0) &=& P_{j0}(\mbox{\bf... ...{j,\nu-1}}(\mbox{\bf x}_0) &=& P_{j,\nu-1}(\mbox{\bf x}_0) %%\\ \end{eqnarray*}$$

es decir, para cada $k\in[\![0,\nu-1]\!]$ se han de aplicar consecutivamente las compuertas $Q^c_{\ell,\varepsilon_{j,k-\ell}}$, con $\ell=0,\ldots,k$, la cual selecciona a los dígitos en la representación binaria de $j$ yendo del más significativo hacia el menos significativo.

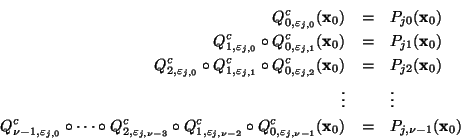
Así pues, será necesario utilizar los operadores reverso para intercambiar el orden de los bits de cada índice $j\in[\![0,2^{\nu}-1]\!]$.

Ahora bien, cada bit $\varepsilon$ se representa por el vector básico $\mbox{\bf e}_{\varepsilon}$. Así que cada operador controlado $Q^c_{k,\varepsilon}$, cuyo dominio es $\mathbb{H}_1$ puede identificarse con el operador $\mbox{\bf x}\mapsto Q^{c2}(\mbox{\bf x},\mbox{\bf e}_{\varepsilon})$ donde

$$Q^{c2} = (I\otimes Q_k)\circ C \circ (I\otimes Q_k^H)\circ C \circ (Q_k\otimes I).$$ (10)

El algoritmo para calcular la transformada de Fourier es entonces el siguiente:

Entrada.

$n=2^{\nu}$, $\mbox{\bf f}\in\mathbb{C}^n=\mathbb{H}_{\nu}$.

Salida.

$\hat{\mbox{\bf f}}=\mbox{TDF}(\mbox{\bf f})\in \mathbb{H}_{\nu}$.

Procedimiento

TDF $(n,\mbox{\bf f})$

1. Sea $\mbox{\bf x}_0:=H(\mbox{\bf e}_0)$.
2. Para cada $j\in[\![0,2^{\nu}-1]\!]$, o equivalentemente, para cada $\left(\varepsilon_{j,\nu-1}\cdots \varepsilon_{j,1}\varepsilon_{j,0}\right)\in\{0,1\}^{\nu}$, hágase en paralelo:
   1. Para cada $k\in[\![0,\nu-1]\!]$ hágase en paralelo:
      1. Sea $\mbox{\boldmath$\delta$}:=R_k\left(\left.\mbox{\boldmath$\varepsilon$}_j\right\vert _k\right)$ el reverso de la cadena formada por los $(k+1)$ bits menos significativos (véase la ec. (5)).
      2. Sea $\mbox{\bf y}_{jk}:=\mbox{\bf x}_0$.
      3. Para $\ell = 0$ hasta $k$ hágase { $\mbox{\bf y}_{jk}:=Q^{c2}(\mbox{\bf y}_{jk},\mbox{\bf e}_{\delta_{j,\ell}})$ (véase la ec. (10)) }
   2. Sea $\mbox{\bf y}_{j}:=\mbox{\bf y}_{j0}\otimes \cdots \otimes\mbox{\bf y}_{j,\nu-1}$ (véase la ec. (8)).
3. Dése como resultado $\hat{\mbox{\bf f}}= \sum_{j=0}^{2^{\nu}-1} f_j\mbox{\bf y}_{j}$.

El cálculo de la transformada inversa discreta de Fourier, TIDF $(n,\mbox{\bf f})$ se hace de manera similar cambiando la matriz $Q_k$ por su hermitiana $Q_k^H$ que sólo involucra el cambio de signo en la potencia de su elemento $(2,2)$.

Posterior: Algoritmo de Shor Arriba: Un poco de computación Anterior: Algoritmo de Deutsch-Jozsa