| (1) |
Harold V. McIntosh
Escuela Superior de Fisica y Matematicas,
Instituto Politecnico Nacional,
Mexico 14, D.F. Mexico
Instituto Nacional de Energia Nuclear,
Avenida Insurgentes Sur 1079,
Mexico l8, D.F. Mexico
One of the traditional puzzles for students of quantum mechanics is the reconciliation of the quantification principle that wave functions must be square integrable with the reality that continuum wave functions do not respect this requirement. By protesting that neither are they quantized the problem can be sidestepped, although some ingenuity may still be required to find suitable boundary conditions. Further difficulties await later on when particular systems are studied in more detail. Sometimes all the solutions, and not just some of them, are square integrable. Then it is necessary to resort to another principle, such as continuity or finiteness of the wave function, to achieve quantization. Examples where such steps have to be taken can be found both in the Schrödinger equation and the Dirac equation. The ground state of the hydrogen atom, the hydrogen atom in Minkowski space, the theta component of angular momentum, all pose problems for the Schrödinger equation. Finiteness of wavefunction alone is not a reliable principle because it fails in the radial equation of the Dirac hydrogen atom. Thus the quantizing conditions which have been invoked for one potential or another seen to be quite varied.
Singular potentials, the criteria for which vary somewhat between the Schrödinger equation, the Dirac equation, and the Klein-Gordon equation, originate another variant of the quantization problem. Continuum wave functions forming the positive energy states of a potential which vanishes at large distances may not be square integrable, but they are at least irredundant in the sense of linear independence in a vector space. Singular potentials exhibit another type of continuum, wherein every energy possesses square-integrable solutions to the wave equation, but they are all linearly dependent on a discrete subset. It is often felt that such potentials are ``unphysical'' but the appelation is neither true nor particularly admissible as a pretext for not understanding the mathematical properties of such solutions. Physical occurrences of such potentials include the Dirac equation for superheavy nuclei the ground states of magnetic monopoles, and higher multipole approximations to ordinary potentials. Even if magnetic monopoles do not exist, the same difficulty is still to be found in all the higher multipoles; for instance in electric dipoles.
One wonders why the requirement of square-integrability as the condition of quantization should be so prevalent? No doubt a substantial part of the reason is pedagogical. Square integrability is a rather dramatic characteristic of the solutions of a wave equation, fairly easy to explain in terms of probability, and quite in accordance with the historical development of the philosophy of quantum mechanics. Once students are convinced of the importance of square integrability, the foundations of the course have been laid, and the applications can begin. To dwell further on the foundations, particularly if much mathematics is required, disturbs the balance between speculation and results, and so the matter is usually not pursued further. By the time that the really important discrepancies begin to occur, the simple statement of the quantization principle has become so ingrained as an inviolable axiom, much as happens to the ``no crossing'' rule, that it is hard to return to basic principles.
If square integrability is not an adequate principle, what really is the principle? For an understanding of this point it seems desirable first to separate quantum dynamics from quantum observability.
Observations are described with the aid of wave functions, in the sense that the square of the amplitude of a wave function is taken to be the probability density for finding a particle, or perhaps an assemblage of particles, in a certain place at a certain time. Properties of the system, such as its energy, its momentum, or some other physical characteristic can be calculated from the wave function by means of a bilinear form and appropriate operators For such calculations to be possible, the wave functions have to satisfy certain restrictions; for example square integrability is the requirement that there be a unit probability of finding the particle somewhere, anywhere. Consequently the requirement that wave functions should belong to Hilbert space has been widely taken as a basic principle of quantum mechanics. A whole theory of probability is then overlaid on this Hilbert space: the elementary probabilities are taken from bilinear operators on the Hilbert space, following which their origin is of no great concern.
Dynamics, on the other hand, is described by a wave equation, which follows out the temporal development of the wave functions. Even if the system is static, its stasis is described in a special way, by a time-independent wave equation. There are two styles which can be used for this description: operators or functional analysis. On the one hand there is matrix mechanics or the ``Heisenberg picture'', while on the other there are partial differential equations comprising wave mechanics and the ``Schrödinger picture''. The choice between these is a matter of taste, although somethings are better expressed one way and others in the other. Differential equation theory tends to be more concrete and computational, giving specific examples and information, while functional analysis allows the information to be summarized from an algebraic viewpoint, dealing with dimensions of solution spaces, mappings between them, and so on.
Having established dynamics and interpretation as two distinct phases of quantum mechanics, the discrepancies between the two have to be taken into account. At the same time it is possible to locate the ``quantization principle'' and to identify the source of confusion with respect to its application. It is essential to observe that dynamics and interpretation work with two different structures having quite different characteristics. Dynamics is a local theory, dealing with differential equations and derivatives, boundary values and initial conditions, and such like. Interpretation is a global theory, dealing with integrals and integrability, functions and bases, probabilities and statistics. In turn, dynamics can be taken as an expression of the automorphisms of the function spaces of interpretation theory.
The quantization principle is that solutions of the dynamical equations must form a basis for the Hilbert space upon which the interpretation is performed.
Most of the confusion to which we have alluded arises from supposing that a basis for Hilbert space either must or ought to belong to Hilbert space.
The selection of a basis for Hilbert space is an old story. Physicists distinguish ``wave functions'' and ``wave packets'' for just this reason, although the way the motivation is usually stated is that they wish to localize their particle. A plane wave may satisfy the Schrödinger equation, but cannot represent a particle because it has a constant amplitude everywhere, even at very remote distances. A Fourier synthesis of plane waves may localize the particle, evidenced by the square integrability of the represented function.
Even though a Hilbert space basis of wave packets could be built up, it is still conceptually simpler to think in terms of plane waves.
Probably the reason that this distinction was lost pedagogically was to avoid burdening an elementary exposition with all the machinery of Fourier analysis, especially in those applications where bound states predominate, and a single solution is at once square integrable and stationary. Mathematical authors of books on Hilbert space have not particularly aided the cause, because of their proclivity for self-contained axiomatic systems. Hilbert space bases of Hilbert space are given a careful analysis, bounded operators receive a preferential treatment; but even such fundamental operators as the derivative wreak havoc with such a restricted theory. Such theories were not precisely what was needed.
Historically the different approaches of Dirac and von Neumann illustrate the contrast between a formalistic but readily usable approach and a mathematically accurate but somewhat complicated exposition. The growth of Schwartz' distribution theory has reconciled many of the technical discrepancies between those two extremes of approach, but the real difficulty has always been more philosophical or conceptual. From the beginning there has been fairly adequate mathematical machinery available once it was clear on what to use it, notably in the form of the theory of the Stieltjes integral.
At least for situations in which the dynamical equation can be written as a set of ordinary linear differential equations there is a very interesting explicit construction connecting the interpretation space of square integrable functions and the solution space for a set of differential equations. The construction originated with Weyl's dissertation [1] of 1910, played an important role in Schrödinger's formulation of his explanation of quantization, and eventually received an extended application when Titchmarsh and a series of his students began to generalize these concepts at mid-century. These trends were analyzed in Loebl's third volume [2] of Group Theory and its Applications which should be consulted as a predecessor to the present article.
In the Loebl article a single second order differential equation was chosen as an example, because it sufficed to explain how Green's formula establishes a mapping between function space and the space of boundary values for a differential equation. Such a low dimension simplifies the exposition, but at the same time there occur some obscuring simplifications. The fact that Green's function is a scalar is one of them, the fact that some aspects are elegantly formulated in terms of analytic functions of a single complex variable is another.
To present a discussion of some of the details of the higher order systems for Per-Olov Löwdin's anniversary volume somehow seems appropriate, because they involve group theory, projection operators, matrix partitioning, and long forgotten papers which somehow contain all that a contemporary young mathematician could desire.
Birkhoff and Langer [3] showed how to apply Sturm Liouville theory to systems of first order ordinary differential equations, with the objective to expand functions defined over an interval in terms of the eigenfunctions of the system over the same interval. For purposes of discussion, as well as for numerical integration, the system could be written in standard form
| (1) |
To obtain Green's formula or the Lagrange identity, an adjoint equation is needed, and will generally require a matrix coefficient for the derivative term. For that reason the canonical form of the equation can be introduced:
| (2) |
When F and R are zero, the equation is called homogeneous; otherwise inhomogeneous. If the homogeneous equation 2) is written in operator form
| (3) |
Obviously, if
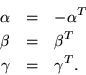
By direct substitution it can be established that
Once the adjoint of an operator has been properly defined, Green's formula follows from a straightforward calculation with two vector solutions ![]() and
and ![]() .
.
| (4) |
The formula can be given a real or complex form according to whether the symmetric or the hermitean transpose are used. Moreover, if these vectors are eigenfunctions,
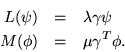
Then
| (5) |
For real solutions belonging to equal eigenvalues this formula expresses a conservation equation. For a single second order equation it expresses the constancy of the Wronskian of two solutions, whereas in general it states the constancy of a bilinear version of the Wronskian of two solutions, from which other multilinear invariants, including the Wronskian, can be deduced. It is more interesting that when ![]() and
and ![]() are matrices, the result states that the solution matrices conserve a certain bilinear form much as orthogonal matrices conserve distance. The important difference is that the conserved bilinear form is antisymmetric rather than positive definite, so that the solution matrix is required to be symplectic. This condition is particularly evident when the system is written in canonical form and
are matrices, the result states that the solution matrices conserve a certain bilinear form much as orthogonal matrices conserve distance. The important difference is that the conserved bilinear form is antisymmetric rather than positive definite, so that the solution matrix is required to be symplectic. This condition is particularly evident when the system is written in canonical form and ![]() is the constant unit antisymmetric matrix.
is the constant unit antisymmetric matrix.
Symplectic matrices have characteristic properties, just as do unitary and orthogonal matrices. Their eigenvalues occur in reciprocal pairs with equal multiplicities. Their eigenvectors are orthogonal with respect to the metric matrix ![]() .
These results are not as dramatic as for unitary or orthogonal matrices because the eigenvalues do not need to have absolute value 1, so that a set of symplectic matrices would not usually generate a compact group. Nevertheless they are necessary and sufficient conditions for a complete characterization, and they do have some further consequences. For example, one conclusion is that of 2p linearly independent solutions over a semiinfinite interval, at least p of them must be square integrable, a result which is important for developing the theory further.
.
These results are not as dramatic as for unitary or orthogonal matrices because the eigenvalues do not need to have absolute value 1, so that a set of symplectic matrices would not usually generate a compact group. Nevertheless they are necessary and sufficient conditions for a complete characterization, and they do have some further consequences. For example, one conclusion is that of 2p linearly independent solutions over a semiinfinite interval, at least p of them must be square integrable, a result which is important for developing the theory further.
Green's formula is the link through which many properties of the solution of a system of differential equations may be established by allowing passage between function space and boundary value space, quite aside from its use in establishing the symplectic nature of the solution matrix for the system. Perhaps the next interesting result after Green's formula is the derivation of Green's function, which relates the solutions of an inhomogeneous equation to the inhomogeneous term and the solutions of the corresponding homogeneous equation. Green's functions have been determined for an extremely wide variety of differential equations. For this, it seems strange that the explicit form for a first order matrix equation is not more readily accessible, but it does not seem to be found in several of the more widely used textbooks.
It is well known that if
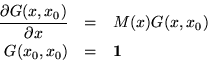
| (6) |
If the canonical form were used instead, we would have to write
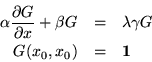
To solve a Sturm-Liouville, boundary value problem, we would begin by referring the value of the solution at an arbitrary point to the boundary values at the points a and b:
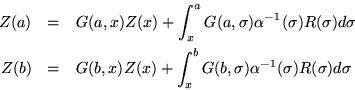
However, boundary conditions are probably more interesting than boundary values but they can be accommodated by using the metric matrix ![]() and suitable vectors
and suitable vectors ![]() and
and ![]() .
We require
.
We require
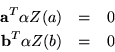
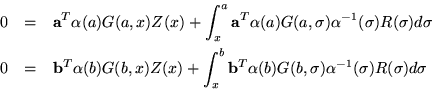
The subsequent results are not affected by the fact that these two matrices are not unique.
After a bit of study we arrive at the result
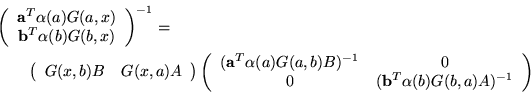
In order to simplify several subsequent formulas it is convenient to introduce the definitions
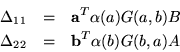
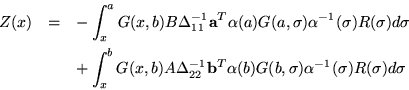
| (8) |
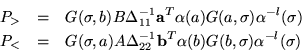
First, we get the multiplication table
Having two orthogonal idempotents makes us curious about their sum. Fortunately the sum is readily obtainable by observing that
This result is necessary to verify explicitly that equation 7 gives a solution to the inhomogeneous equation, and it is also worthwhile to note that it is just the discontinuity of Green's matrix for coincident arguments. Such an irregularity is well known for scalar Green's functions; they are continuous up to a certain order, but then have a delta function discontinuity in their last derivative.
The derivation just given is valid for any system of equations, self-adjoint or not, and for any assignment of boundary conditions to one or the other of the two endpoints. Even so, the formulas have a fairly plausible interpretation. Denominators such as
![]() refer to the projection of a solution starting from one of the boundary points on the boundary condition, calculated from the adjoint equation, taken from the other endpoint. According to Green's formula this inner product will be the same no matter the interior point at which it is calculated, and it will vanish only when some initial value at one end gives a solution which meets the boundary condition at the other end. This is in accord with the dichotomy, that whenever the Sturm-Liouville problem has a solution, the inhomogeneous equation does not, and conversely.
refer to the projection of a solution starting from one of the boundary points on the boundary condition, calculated from the adjoint equation, taken from the other endpoint. According to Green's formula this inner product will be the same no matter the interior point at which it is calculated, and it will vanish only when some initial value at one end gives a solution which meets the boundary condition at the other end. This is in accord with the dichotomy, that whenever the Sturm-Liouville problem has a solution, the inhomogeneous equation does not, and conversely.
When the system of equations is self-adjoint, the boundary values and the boundary conditions satisfy the same differential equation, even though they evolve from possible different initial conditions and hence would not coincide. Anyway, if more conditions were specified at one end than at the other, matrices of two different dimensionalities would be involved. Thus there is a further configuration of high symmetry, wherein half of the boundary conditions are specified at one end and half at the other. At each endpoint the antisymmetric matrix ![]() is a metric matrix for a symplectic geometry, and it may happen that the boundary conditions lie in a maximal isotropic subspace for such a metric. In that case, boundary values would simultaneously serve as boundary conditions. The very highest symmetry would then arise when the two kinds of solutions were considered to be identical, with no distinction between initial value and initial condition.
is a metric matrix for a symplectic geometry, and it may happen that the boundary conditions lie in a maximal isotropic subspace for such a metric. In that case, boundary values would simultaneously serve as boundary conditions. The very highest symmetry would then arise when the two kinds of solutions were considered to be identical, with no distinction between initial value and initial condition.
Indeed, this is the situation most familiar to persons experienced with Green's functions, which are often visualized as products of functions meeting the respective boundary conditions and normalized to have a unit irregularity at their point of crossing. To further compare the derivation just given with a familiar situation, it might be noticed that the self-adjoint form of a second order differential operator
For the Schrödinger equation the coefficient matrix ![]() is degenerate, although still symmetric. The bilinear form in function space therefore depends only on the wave function and not on its derivative. For the Dirac equation, we have to use the sum of the squares of the two components, likewise a familiar result.
is degenerate, although still symmetric. The bilinear form in function space therefore depends only on the wave function and not on its derivative. For the Dirac equation, we have to use the sum of the squares of the two components, likewise a familiar result.
A self adjoint system of differential equations with canonical boundary conditions is particularly well suited to a discussion of the theory of singular differential equations, because the canonical boundary conditions are already compatible with the definition of the Weyl circle, or its generalization to a higher order system as a maximal isotropic subspace. The details of this generalization may be found in any of the standard references, or in Loebl's third volume [2]. Nevertheless, there is a further detail, the application of this theory to a doubly infinite interval, which has an interesting connection with Green's function, and which is well to bring out this time.
To overcome difficulties of normalizing functions which have a nonzero amplitude over all of an interval which tends to infinity, it is helpful to describe eigenfunction expansions in terms of a Stieltjes integral. For all finite intervals the distribution function of this integral is a step function, whose limiting behaviour is pertinent to the spectral classification of the differential system over an infinite interval. A system of 2p differential equations will allow an eigenfunction expansion of not only scalar functions defined over the solution interval, but even vector valued functions up to dimension 2p. An expansion formula would be expected to have the form -
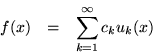
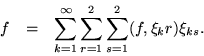
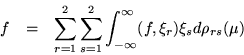
One way of determining the spectral matrix is to expand some known function with the hope of isolating its coefficients. In the process, Green's formula may be used to reduce the integral over function space to a sum over the boundary values. Moreover, if the function chosen for expansion belongs to the Weyl surface, the terms which belong to the endpoints will drop out, freeing the formula from an explicit dependence on the endpoints. An implicit dependence remains, because the Weyl surface determines the Sturm-Liouville boundary conditions to be used, but even these vestiges disappear when real boundary conditions are invoked.
It is rare that the same function will belong to the Weyl surfaces at both ends of the two-sided interval, so that the expansion formula would best be applied to a composite function which solves the system of equations in each of two subintervals and has a joining discontinuity at an internal initial point. All integrals would be written as a sum of two parts, for each of which Green's formula would be individually valid.
Finally, it is slightly simpler to apply Green's formula to the Parseval equality rather than to the expansion formula. Taking all this into account, we begin by writing
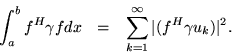
From the left side:
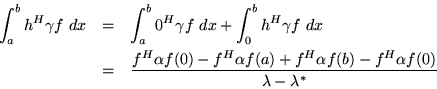
Similarly,
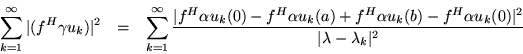
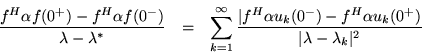
Since the spectral density matrix is divided naturally into quadrants, some algebraic maneuvering and a careful choice of f's is required to obtain the separate quadrants. If we take
| (9) |
The choice of
| (10) |
The off-diagonal block can be gotten from a consideration of
![]() ,
which follows a similar expansion and leads to
,
which follows a similar expansion and leads to
| (11) |
It is an interesting result that these expressions are just the discontinuities in Green's matrix along its diagonal. Therefore we can say that the imaginary part of the discontinuity in the complex Green's matrix is the spectral density function, while the discontinuity in the real Green's matrix is merely ![]() .
This explains why the complex poles of Green's function and the poles of the spectral density are the same; both depend on the same denominator
(Ma-Mb)-1.
.
This explains why the complex poles of Green's function and the poles of the spectral density are the same; both depend on the same denominator
(Ma-Mb)-1.
By and large the generalization for a system of equations of Weyl's spectral theory provides the link which is needed between Hilbert space theory and differential equation theory. By the use of such devices as hyperspherical harmonics or separation of variables many quantum mechanical systems can be reduced directly to this form. At the same time, it might be expected that a fairly explicit theory could be developed directly for partial differential equations. In this respect, the use of functional analysis offers a good idea of what to expect. Nevertheless, the principal advantage of a concrete theory such as Weyl's would seem to be the lessons which it teaches us about the diversity of bases for function spaces which can occur in practice, and the danger of supposing that just one type of basis function - the bound state wave function - is typical of them all.
If Weyl's theory is capable of clarifying our philosophical understanding of quantum mechanics, we might go on to ask whether it has any merit as a numerical procedure? By studying the behavior of |Ma Mb|| we have a single scalar function whose zeroes locate the eigenvalues over a finite interval, and whose limiting behaviour will give us some idea of the nature of the spectrum. It is of some advantage that Ma and Mb, can be obtained as solutions of a Ricatti equation, but equally disadvantageous if they have to be obtained from complex eigenvalues, because of the fourfold increase in real multiplications involved.
In summary, we have called attention to the vexing problem of explaining just what is the quantization condition for quantum mechanics, and indicated that the extension of Weyl's second order theory of differential equations to systems of equations can be given a particularly elegant formulation which does not seem to be mentioned in any of the common differential equations textbooks. There still remains the explicit demonstration of the correctness of this interpretation through the exhibition of the resolution of a variety of typical examples, which may have to be put off until a subsequent birthday.