



Siguiente: Supresión de producciones vacías
Un nivel arriba: Transformaciones equivalentes de gramáticas
Anterior: Transformaciones equivalentes de gramáticas
Un símbolo variable 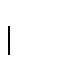 se dice ser útil si aparece en el transcurso de una derivación terminal, a partir del símbolo inicial. Es decir, si
se dice ser útil si aparece en el transcurso de una derivación terminal, a partir del símbolo inicial. Es decir, si
Un símbolo es inútil (¿qué más?) si no es útil.
Proposición 2.1
Toda gramática libre de contexto
G=(V,T,P,S) se puede transformar en una gramática libre de contexto
G'=(V',T,P',S') equivalente a G sin variables inútiles.
Para demostrar esta proposición es necesario, primero, reducir la gramática dada a una gramática en la que todo símbolo variable derive una palabra terminal. Se ha de ver luego que tal gramática reducida puede a su vez reducirse a otra en la que cualquier símbolo variable aparece en alguna cadena derivable a partir del símbolo inicial.
Al componer ambas transformaciones se tendrá la gramática cuya existencia se proclama en la proposición.
Lema 2.1 (Búsqueda hacia atrás)
Toda gramática libre de contexto
G=(
V,
T,
P,
S), con
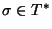
,
se puede transformar en una gramática libre de contexto
G'=(
V',
T,
P',
S') equivalente a
G tal que para cualquier
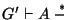
existe
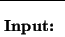
con la propiedad
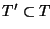
.
En efecto, primeramente consideremos como buenas a las variables que generan palabras terminales en un solo paso, es decir, a aquellas que aparecen como antecedentes de producciones cuyos consecuentes son palabras terminales, incluso la vacía. Reiteremos este procedimiento, considerando como buenas a las variables que aparecen como antecedentes de producciones cuyos consecuentes son palabras sobre símbolos terminales o variables ya consideradas como buenas. El total de variables buenas da la gramática reducida que se busca.
En la figura 6.1 presentamos un seudocódigo de este procedimiento.
Figure 6.1:
Búsqueda hacia atrás: Reducción a gramáticas cuyas variables todas derivan palabras terminales.
|
|
Lema 2.2 (Búsqueda hacia adelante)
Toda gramática libre de contexto
G=(
V,
T,
P,
S), se puede transformar en una gramática libre de contexto
G'=(
V',
T',
P',
S') equivalente a
G tal que
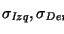
y para cualquier símbolo
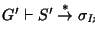
existen
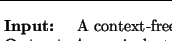
con la propiedad

.
En efecto, ahora, primeramente consideremos como buenos a los símbolos que se generan a partir del inicial en un solo paso, es decir, a aquellos que aparecen en consecuentes de producciones cuyo antecedente es el símbolo inicial. Reiteremos este procedimiento, considerando como buenos a los símbolos que aparecen en consecuentes de producciones cuyos antecedentes son símbolos ya consideradas como buenos. El total de símbolos buenos da la gramática reducida que se busca.
En la figura 6.2 presentamos un seudocódigo de este procedimiento.
Figure 6.2:
Búsqueda hacia adelante: Reducción a gramáticas cuyas variables todas se derivan a partir del símbolo inicial.
|
|
Si se aplica primero el lema 6.2.1 y luego el 6.2.2 a una gramática dada, se convierte ésta en una gramática equivalente sin símbolos inútiles. Si el orden de aplicación se invierte, i. e. primero se aplica el lema 6.2.2 y luego el 6.2.1, entonces no necesariamente se eliminan los símbolos inútiles, como se puede ver considerando la gramática
Si aplicamos 6.2.1 obtenemos la gramática
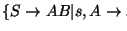 y luego al aplicar 6.2.2 obtenemos
y luego al aplicar 6.2.2 obtenemos
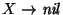 ,
la cual ya no tiene símbolos inútiles.
Recíprocamente, si aplicamos 6.2.2 obtenemos la gramática
,
la cual ya no tiene símbolos inútiles.
Recíprocamente, si aplicamos 6.2.2 obtenemos la gramática
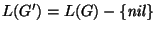 y luego al aplicar 6.2.1 obtenemos
y luego al aplicar 6.2.1 obtenemos
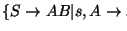 ,
la cual contiene al símbolo inútil A.
,
la cual contiene al símbolo inútil A.




Siguiente: Supresión de producciones vacías
Un nivel arriba: Transformaciones equivalentes de gramáticas
Anterior: Transformaciones equivalentes de gramáticas
Guillermo Morales-Luna
2000-06-27
 se dice ser útil si aparece en el transcurso de una derivación terminal, a partir del símbolo inicial. Es decir, si
se dice ser útil si aparece en el transcurso de una derivación terminal, a partir del símbolo inicial. Es decir, si
 .
.