![$\begin{array}[t]{rcl}
\mbox{\it tran\/}(q_0,m_{5}p_1) &=& q_0 \\
\mbox{\it res\/}(q_0,m_{5}p_1) &=& s_3
\end{array}$](img651.gif) |
si se inserta una moneda de $5 pesos y no hay cambio, se devuelve la moneda y se reinicia el proceso, |
![$\begin{array}[t]{rcl}
\mbox{\it tran\/}(q_0,m_{5}P) &=& a_0 \\
\mbox{\it res\/}(q_0,m_{5}P) &=& s_2
\end{array}$](img652.gif) |
si hay monedas en la alcancía, i.e. 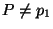 ,
entonces se da el peso de cambio, ,
entonces se da el peso de cambio, |
![$\begin{array}[t]{rcl}
\mbox{\it tran\/}(q_0,m_{2}P) &=& b_2 \\
\mbox{\it res\/}(q_0,m_{2}P) &=& s_0
\end{array}$](img654.gif) |
se insertan $2 pesos y se espera a completar el importe de $4 pesos, |
![$\begin{array}[t]{rcl}
\mbox{\it tran\/}(b_2,m_{2}P) &=& q_0 \\
\mbox{\it res\/}(b_2,m_{2}P) &=& s_1
\end{array}$](img655.gif) |
habiéndose completado el costo de la golosina, se lo entrega y se reinicia el proceso, |
![$\begin{array}[t]{rcl}
\mbox{\it tran\/}(b_2,m_{1}P) &=& c_1 \\
\mbox{\it res\/}(b_2,m_{1}P) &=& s_0
\end{array}$](img656.gif) |
se inserta un peso más y hay que esperar a que llegue el último, |
![$\begin{array}[t]{rcl}
\mbox{\it tran\/}(b_2,MP) &=& b_2 \\
\mbox{\it res\/}(b_2,MP) &=& s_3
\end{array}$](img657.gif) |
si llega una moneda con denominación mayor
M=m5,m10 entonces se la devuelve y se continúa la espera, |
![$\begin{array}[t]{rcl}
\mbox{\it tran\/}(q_0,m_{1}P) &=& c_3 \\
\mbox{\it res\/}(q_0,m_{1}P) &=& s_0
\end{array}$](img658.gif) |
si se inicia el pago con una moneda de un peso hya que esperar los otros tres pesos, |
![$\begin{array}[t]{rcl}
\forall k=3,2,1:&& \\
\mbox{\it tran\/}(c_{k},m_{1}P) &=& c_{k-1} \\
\mbox{\it res\/}(c_{k},m_{1}P) &=& s_0
\end{array}$](img659.gif) |
se continúa el pago, recibiendo un peso a la vez. Aquí c0=a0. Si se recibe monedas de mayor denominación, se develve éstas. |
| |
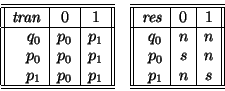
cualquier otra posibilidad
(Estado,Entrada)
es inconsistente e inalcanzable en la máquina. |

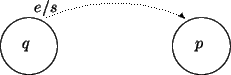
, y recibe una literal de entrada
, entonces emite el símbolo de salida
y transita al nuevo estado
.



![\begin{eqnarray*}q_0 &:& \mbox{\rm estado inicial}, \\
\forall i\in[0,5]:a_i &...
...por pagar $k$\space pesos cuando se inici\'o el pago con \$1.}
\end{eqnarray*}](img643.gif)
![\begin{eqnarray*}\forall i\in[1,6]:p_i &:& \mbox{\rm NO alcanza a haber $i$\space pesos,} \\
p_7 &:& \mbox{\rm al menos hay \$6 pesos.}
\end{eqnarray*}](img644.gif)