Siguiente: Equivalencia e indistinguibilidad Un nivel arriba: Máquinas secuenciales Anterior: Máquinas de Mealy

Máquinas de Moore

Una máquina de Moore es similar a una de Mealy, salvo en que la respuesta sólo depende del estado actual de la máquina y es independiente de la entrada. Precisamente, una máquina de Moore es una estructura de la forma

$$\mbox{\it MMo\/}=(Q,\mbox{\it Ent\/},\mbox{\it Sal\/},\mbox{\it tran\/},\mbox{\it res\/},q_0)$$

donde

$$\begin{eqnarray*}Q &:& \mbox{\rm es el conjunto de {\em estados},} \\ \mbox{\i... ...ta},} \\ q_0\in Q &:& \mbox{\rm es el estado {\em inicial}.} \end{eqnarray*}$$

La semántica procedimental de la máquina de Moore es la siguiente:

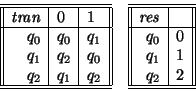
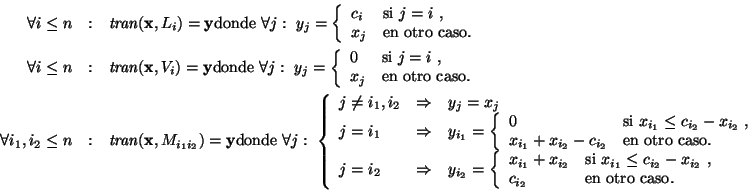Al inicio de cualquier computación, la máquina se encuentra en el estado q₀. Posteriormente, cuando la máquina se encuentra en un estado $q\in Q$, y recibe una literal de entrada $e\in\mbox{\it Ent\/}$, entonces transita al nuevo estado $p=\mbox{\it tran\/}(q,e)$ y emite el símbolo de salida $s=\mbox{\it res\/}(p)$.

Ejemplos 1. Congruencias módulo 3: Supongamos que se da un número $n\in I\!\!N$ en su representación binaria y se quiere calcular su residuo módulo 3. Consideremos la máquina cuya representación gráfica se muestra en la figura (3.3).

  

Figure 3.3: Máquina de Moore para calcular congruencias módulo 3 de números dados en binario.

Las funciones de transición y de respuesta quedan especificadas de manera tabular como sigue:

$$\begin{array}{c@{\ \ \ }c} \begin{array}{\vert\vert r\vert l... ...q_1 & 1 \\ q_2 & 2 \\ \hline\hline \end{array} \end{array}$$

Por inducción en la longitud n de cualquier palabra $\sigma\in (0+1)^*$, que sea la representación en binario de un número $x_{\sigma}$ se puede ver que la respuesta final obtenida al aplicar $\sigma$ es $x_{\sigma}\mbox{\rm mod }3$. En efecto, para n=1, con las palabras '0' y '1' se tiene las respuestas correctas 0 y 1. Sea n>0. Supongamos que para una palabra $\sigma$, de longitud n-1, se tiene como respuesta final i, donde $x\equiv i\mbox{\rm mod }3$ y x es el número representado en binario por $\sigma$. Para $s\in(0+1)$ el número representado por la concatenación de $\sigma$ con s, $\sigma s$ es 2x+s, el cual es congruente módulo 3 con $2i+s\mbox{\rm mod }3$. Al tabular estos últimos valores se tiene

$$\begin{array}{\vert\vert c\vert l\vert l\vert\vert}\hline\hli... ... & 1 \\ 1 & 2 & 0 \\ 2 & 1 & 2 \\ \hline\hline \end{array}$$

lo que corresponde naturalmente a la tabla de transiciones del autómata construído. De hecho, éste es un caso particular del siguiente ejemplo más general: Sea n>1 una base de representación de números naturales y sea k>0 un número natural. Sea $\mbox{\it MMo\/}_{\mbox{\scriptsize mod }k}^n$ la máquina de Moore tal que

• posee n símbolos de entrada $\{0,\ldots,n-1\}$,
• posee k estados $\{q_0,\ldots,q_{k-1}\}$, y k símbolos de salida, uno por cada estado.
• tiene como transición a la función $(q_i,s)\mapsto q_{(i\cdot n)\mbox{\scriptsize mod }k}$, y
• tiene como respuesta $q_i\mapsto i$.

Entonces $\mbox{\it MMo\/}_{\mbox{\scriptsize mod }k}^n$ calcula el residuo módulo k de cualquier número en base n. En la tabla (3.3) presentamos las tablas de transición de las máquinas $\mbox{\it MMo\/}_{\mbox{\scriptsize mod }k}^{10}$, para k=5,7,13.

  

Table 3.3: Cálculo de residuos módulo 5, 7 y 13 en notación decimal.

El lector no ha de tener dificultad en visualizar, a partir de esos ejemplos, las transiciones de cualquier máquina $\mbox{\it MMo\/}_{\mbox{\scriptsize mod }k}^n$.


2. Problema de botes: Supongamos dados k>1 botes. Para cada $i\leq k$, sea $c_i\in I\!\!N$ la capacidad, en litros, del i-ésimo bote. Los botes pueden ser llenados de agua o bien ser vaciados de acuerdo con las siguientes reglas:

Li	:	llénese el i-ésimo bote,
Vi	:	vacíese el i-ésimo bote,
Mi1i2	:	viértase el contenido del i1-ésimo bote en el i2-ésimo hasta que aquel se vacíe o éste se llene.

Si se considera a los dos primeros botes como distinguidos, se trata de caracterizar a las cantidades de agua ``constructibles'' como suma de los contenidos de esos dos primeros botes. Sean pues $\begin{array}[t]{lcrcl} \mbox{\rm Estados} &:& Q &=& \{\mbox{\bf x}=(x_1,\ldot... ...i_2} \\ \mbox{\rm Salidas} &:& \mbox{\it Sal\/} &=& [0,c_1+c_2] \end{array}$ Las transiciones quedan caracterizadas de la siguiente forma:

$$\begin{eqnarray*}\forall i\leq n &:& \mbox{\it tran\/}(\mbox{\bf x},L_i)=\mbox{\... ...{\rm en otro caso. } \end{array}\right. \end{array}\right. \end{eqnarray*}$$

La respuesta es la función $\mbox{\it res\/}:\mbox{\bf x}\mapsto x_1+x_2$.
Siguiente: Equivalencia e indistinguibilidad Un nivel arriba: Máquinas secuenciales Anterior: Máquinas de Mealy