Siguiente: Autómatas finitos
Un nivel arriba: Máquinas secuenciales
Anterior: Máquinas de Moore
Sea
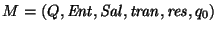 una máquina, ya sea de Mealy o de Moore. Extendemos la función de transición
una máquina, ya sea de Mealy o de Moore. Extendemos la función de transición
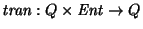 a una función
a una función
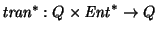 ,
haciendo, para cada estado
,
haciendo, para cada estado 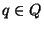 :
:
Así pues, para cada palabra  ,
,
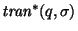 es el estado al que se llega cuando, a partir del estado q, se va aplicando, uno a uno, cada uno de los símbolos de
es el estado al que se llega cuando, a partir del estado q, se va aplicando, uno a uno, cada uno de los símbolos de  ,
de izquierda a derecha.
De manera similar se puede extender la función de respuesta a todo el diccionario
,
de izquierda a derecha.
De manera similar se puede extender la función de respuesta a todo el diccionario
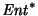 .
Si M es una máquina de Mealy, definimos
.
Si M es una máquina de Mealy, definimos
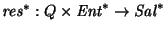 ,
haciendo, para cada estado
,
haciendo, para cada estado 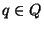 y para cada palabra
y para cada palabra
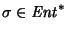 ,
,
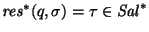 donde,
donde,
en otras palabras, se tiene
Si M es una máquina de Moore, la función de respuesta
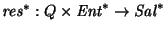 depende únicamente del estado visitado: para cada estado
depende únicamente del estado visitado: para cada estado 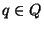
En cualquier caso, sea en máquinas de Mealy o de Moore, la función
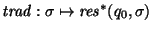 ,
donde q0 es el estado inicial, es la función de traducción que realiza la máquina. Por las semánticas procedimentales introducidas, se tiene que
,
donde q0 es el estado inicial, es la función de traducción que realiza la máquina. Por las semánticas procedimentales introducidas, se tiene que
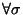 :
:
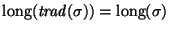 .
.
Dos máquinas M y N se dicen ser equivalentes, 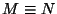 ,
si
,
si
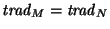 .
En otras palabras, dos máquinas son equivalentes si ambas traducen de idéntica manera a cualquier palabra de entrada.
Ya que las máquinas de Moore son casos particulares de las máquinas de Mealy, se tiene que toda máquina de Moore es equivalente a una de Mealy. Veamos que el recíproco también se cumple:
.
En otras palabras, dos máquinas son equivalentes si ambas traducen de idéntica manera a cualquier palabra de entrada.
Ya que las máquinas de Moore son casos particulares de las máquinas de Mealy, se tiene que toda máquina de Moore es equivalente a una de Mealy. Veamos que el recíproco también se cumple:
Proposición 1.1
Toda máquina de Mealy es equivalente a una de Moore: Para cada máquina de Mealy
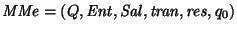
existe una máquina de Moore
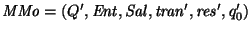
tal que
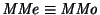
.
En efecto, dada una máquina de Mealy
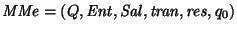 ,
realicemos la siguiente construcción:
,
realicemos la siguiente construcción:
- estados:
- sea
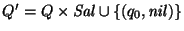 .
Se ``desdobla'' cada estado ''viejo''
.
Se ``desdobla'' cada estado ''viejo'' 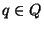 en
en
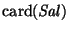 estados ``nuevos'' de la forma (q,t),
estados ``nuevos'' de la forma (q,t),
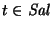 ;
;
- transición:
- sea
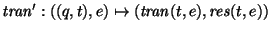 ,
donde tran y res son las funciones de transición y de respuesta ``viejas'';
,
donde tran y res son las funciones de transición y de respuesta ``viejas'';
- respuesta:
- sea
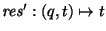 ;
y
;
y
- estado inicial:
- sea
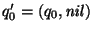 .
.
Se ve directamente que la máquina de Moore construida es equivalente a la de Mealy dada.
Ejemplo
Consideremos la máquina de Mealy del ejemplo 2. anterior que ``reconoce a repeticiones finales de un mismo símbolo en 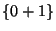 ''. Ahí, la máquina tiene transición y respuesta,
''. Ahí, la máquina tiene transición y respuesta,
La máquina de Moore equivalente consiste de 7=1+6 estados
y sus correspondientes transición y respuesta son
Observamos aquí que los estados
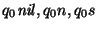 no aparecen en la imagen de la función de transición nueva. Por tanto, los restantes cuatro estados, junto con el inicial, definen una máquina de Moore de 5 estados equivalente a la máquina de Mealy dada.
no aparecen en la imagen de la función de transición nueva. Por tanto, los restantes cuatro estados, junto con el inicial, definen una máquina de Moore de 5 estados equivalente a la máquina de Mealy dada.
En lo que resta de esta sección, consideraremos únicamente máquinas de Moore.
Sea
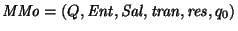 una máquina de Moore. Se dice que
una máquina de Moore. Se dice que
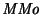 es una máquina-(n,m,k) si
es una máquina-(n,m,k) si
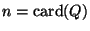 es el número de estados,
es el número de estados,
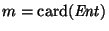 es el número de símbolos de entrada y
es el número de símbolos de entrada y
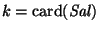 es el número de símbolos de salida, que son efectivamente asumidos bajo la función de respuesta res.
Sea
es el número de símbolos de salida, que son efectivamente asumidos bajo la función de respuesta res.
Sea
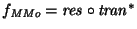 la función que, para un estado q y una palabra
la función que, para un estado q y una palabra  ,
da el último símbolo de respuesta cuando se aplica
,
da el último símbolo de respuesta cuando se aplica  a partir de q.
Diremos que dos estados q1, q2 son indistinguibles,
a partir de q.
Diremos que dos estados q1, q2 son indistinguibles,
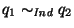 ,
si para cualquier palabra
,
si para cualquier palabra
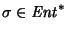 se tiene
se tiene
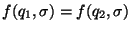 .
Intuitivamente, dos estados son indistinguibles si no se los puede distinguir mediante una sucesión de estímulos, pues ambos estados ofrecen mismas respuestas ante mismas entradas. Los estados son distinguibles si para alguna palabra
.
Intuitivamente, dos estados son indistinguibles si no se los puede distinguir mediante una sucesión de estímulos, pues ambos estados ofrecen mismas respuestas ante mismas entradas. Los estados son distinguibles si para alguna palabra  se tiene
se tiene
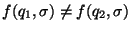 ,
y en tal caso, se dice que
,
y en tal caso, se dice que  los distingue.
los distingue.
Proposición 1.2
Cualesquiera dos estados distinguibles en una máquina-(n,m,k) lo son mediante una palabra de longitud a lo sumo n-k.
En efecto, para cada 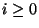 sea Ii el conjunto de parejas de estados que no pueden ser distinguidos por palabras de longitud i,
sea Ii el conjunto de parejas de estados que no pueden ser distinguidos por palabras de longitud i,
Ii es una relación de equivalencia. Sea 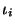 el índice de la relación Ii.
Ya que la sucesión de relaciones
el índice de la relación Ii.
Ya que la sucesión de relaciones 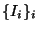 es decreciente, o sea,
es decreciente, o sea,
se tiene que la correspondiente sucesión de índices
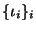 es creciente,
es creciente,
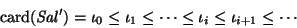 |
(5) |
Naturalmente,
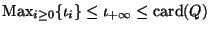 ,
donde
,
donde
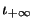 es el índice de la relación ``
es el índice de la relación ``
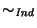 ''.
Por tanto, necesariamente,
''.
Por tanto, necesariamente,
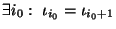 ,
y, de hecho,
,
y, de hecho,
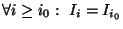 .
De aquí puede verse que las desigualdades intermedias en la serie de relaciones 3.1 son estrictas, es decir
.
De aquí puede verse que las desigualdades intermedias en la serie de relaciones 3.1 son estrictas, es decir
y, en particular,
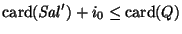 .
Por tanto, el número de relaciones distintas de la forma Ii está mayorizado por la desigualdad
.
Por tanto, el número de relaciones distintas de la forma Ii está mayorizado por la desigualdad
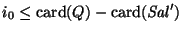 ,
quod erat demonstratum.
,
quod erat demonstratum.
La proposición anterior proporciona un algoritmo elemental para calcular, de manera exhaustiva, al cociente
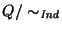 :
:
- 1.
- Sean
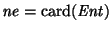 ,
,
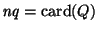 y
y
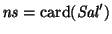 las cardinalidades de los conjuntos de símbolos de entrada, estados y símbolos de salida asumidos.
las cardinalidades de los conjuntos de símbolos de entrada, estados y símbolos de salida asumidos.
- 2.
- Sea
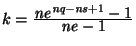 el número de palabras de longitud a lo más
el número de palabras de longitud a lo más
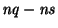 .
.
- 3.
- Fórmese la matriz
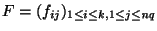 tal que
tal que
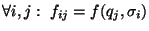 .
.
- 4.
- Dos estados son indistinguibles entre sí si los correspondientes vectores columnas en F coinciden.
Ejemplo. Residuos módulo 4: Una máquina que reconoce números binarios congruentes con 2 o con 4, módulo 4, se muestra en la figura (3.4).
Figure 3.4:
Reconocedor de números binarios congruentes con 2 o 4 módulo 4.
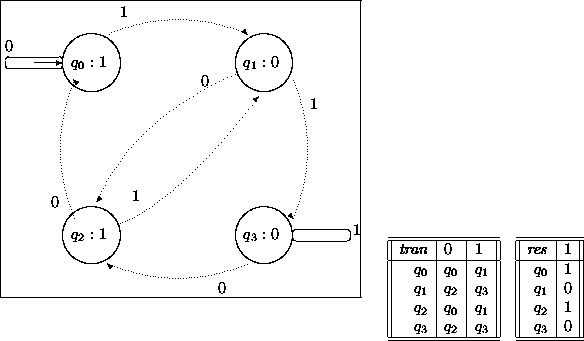 |
Se tiene
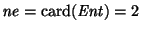 ,
,
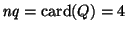 y
y
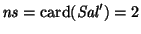 ,
luego
k=24-2+1-1=7.
La tabla para reconocer estados indistinguibles queda:
,
luego
k=24-2+1-1=7.
La tabla para reconocer estados indistinguibles queda:
Por tanto, las parejas
![$[q_0]=\{q_0,q_2\}$](img752.gif) y
y
![$[q_1]=\{q_1,q_3\}$](img753.gif) constan de estados indistinguibles entre sí.
constan de estados indistinguibles entre sí.
Se ve directamente que la relación ``
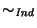 '' es de equivalencia en el conjunto de estados Q. Por tanto, el cociente
'' es de equivalencia en el conjunto de estados Q. Por tanto, el cociente
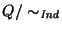 es una partición de Q. Más aún, si dos estados son indistinguibles, lo son también los estados a los que transitan bajo cualquier estímulo,
es una partición de Q. Más aún, si dos estados son indistinguibles, lo son también los estados a los que transitan bajo cualquier estímulo,
en otras palabras, la noción de indistinguibilidad es congruente con las transiciones de la máquina
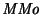 .
.
Observación 1.1
El espacio cociente
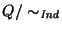
puede ser dotado de una estructura de máquina de Moore.
En efecto, la construcción es la siguiente:
- estados:
- clases de equivalencia
![$[q]\in Q/\sim_{\mbox{\scriptsize\it Ind}}$](img755.gif) ,
con
,
con 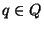 ,
,
- transición:
-
![$\mbox{\it tran\/}_{\mbox{\scriptsize\it Ind}}:([q],e)\mapsto [\mbox{\it tran\/}(q,e)]$](img756.gif) ,
o sea, la clase de indistinguibilidad de q transita, bajo e a la clase del estado al que transita q. Esta definición tiene sentido pues la indistinguibilidad es congruente con las transiciones,
,
o sea, la clase de indistinguibilidad de q transita, bajo e a la clase del estado al que transita q. Esta definición tiene sentido pues la indistinguibilidad es congruente con las transiciones,
- respuesta:
-
![$\mbox{\it res\/}_{\mbox{\scriptsize\it Ind}}:[q]\mapsto \mbox{\it res\/}(q)]$](img757.gif) ,
la cual función también está bien definida, y
,
la cual función también está bien definida, y
- estado inicial:
-
![$q_{0,\mbox{\scriptsize\it Ind}}=[q_0]$](img758.gif) ,
es decir, el nuevo estado inicial es la clase de equivalencia del estado inicial original. En esta clase están incluidos todos los estados indistinguibles respecto a q0.
,
es decir, el nuevo estado inicial es la clase de equivalencia del estado inicial original. En esta clase están incluidos todos los estados indistinguibles respecto a q0.
Así por ejemplo, la máquina cociente del último ejemplo es la siguiente:
Observación 1.2
La máquina cociente tiene un número de estados que no excede al de la máquina dada. De hecho, si hubiera una pareja de estados indistinguibles entonces el número de estados de la máquina cociente es estrictamente menor.
Además, la máquina cociente es equivalente a la máquina dada.
En efecto, veamos que para todo
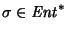 ,
,
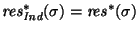 .
Para
.
Para
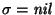 se tiene
se tiene
Ahora, para
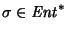 y
y
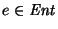 ,
al suponer que
,
al suponer que
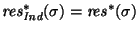 ,
se tiene
,
se tiene




Siguiente: Autómatas finitos
Un nivel arriba: Máquinas secuenciales
Anterior: Máquinas de Moore
Guillermo Morales-Luna
2000-06-27
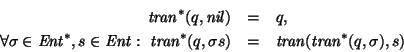
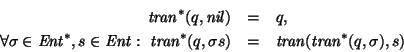
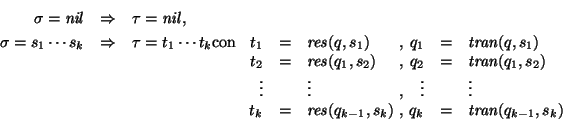
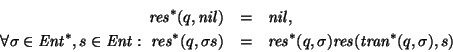
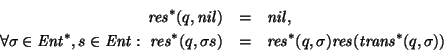
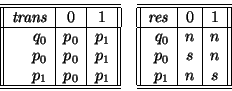


![\begin{picture}(3,1)
\put(0.2,0.5){\vector(1,0){0.3}}
\put(0.75,0.5){\circle...
...(0,0){$[q_1]:0$ }}
\put(2.75,0.5){\oval(.5,.1)}\put(2.75,0.65){1}
\end{picture}](img759.gif)