



Siguiente: Indeterminismo y determinismo
Un nivel arriba: Autómatas no-deterministas
Anterior: Representación de transiciones mediante
El monoide de un autómata no-determinista se construye de manera similar a como se hizo en el caso determinista: Dos palabras
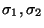 son equivalentes,
son equivalentes,
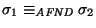 ,
si
,
si
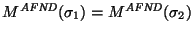 ,
es decir, si ambas definen a la misma relación entre estados.
Esta relación
,
es decir, si ambas definen a la misma relación entre estados.
Esta relación![[*]](../images/spanish/icons.gif/foot_motif.gif) , además de ser de equivalencia, es congruente con la concatenación. Por tanto, el cociente
, además de ser de equivalencia, es congruente con la concatenación. Por tanto, el cociente
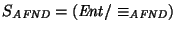 es un monoide, dicho del autómata AFND.
es un monoide, dicho del autómata AFND.
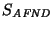 se construye también siguiendo el algoritmo (3.6).
se construye también siguiendo el algoritmo (3.6).
Ejemplo. Aplicando el algoritmo (3.6) al ejemplo anterior, se obtiene las palabras mostradas en la tabla (3.13).
Table 3.13:
Cálculo del monoide del autómata no-determinista.
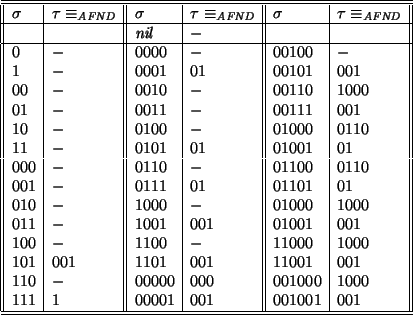 |
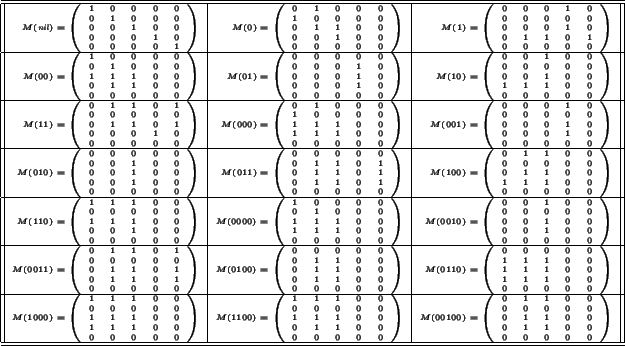
Se ve que exactamente 21 clases de equivalencia conforman el monoide del autómata. En la tabla (3.14) se muestra cada una de las 21 matrices correspondientes.
Table 3.14:
Matrices correspondientes a los elementos del monoide del autómata no-determinista.
 |
Ahí, observamos que las palabras 11 y 0011 son reconocidas por el autómata (sus entradas
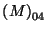 ,
correspondientes a un arribo al estado final q4 a partir del inicial q0, asumen el valor 1). Por tanto, cualquier palabra equivalente a una de ellas dos también ha de ser reconocida. Se tiene pues que el lenguaje reconocido por el autómata no-determinista es precisamente la unión de las dos clases de equivalencia [11] y [0011].
Por otro lado, el monoide del autómata no-determinista puede ser dotado, como se hizo anteriormente, de una estructura de autómata finito. Si aquí se declara como finales a las clases [11] y [0011] entonces el autómata resultante será uno finito que reconoce al mismo lenguaje que el autómata no-determinista. Esta propiedad de ser equivalente a uno finito no es exclusiva del autómata en este ejemplo según veremos en el lema (3.3.2) más abajo.
,
correspondientes a un arribo al estado final q4 a partir del inicial q0, asumen el valor 1). Por tanto, cualquier palabra equivalente a una de ellas dos también ha de ser reconocida. Se tiene pues que el lenguaje reconocido por el autómata no-determinista es precisamente la unión de las dos clases de equivalencia [11] y [0011].
Por otro lado, el monoide del autómata no-determinista puede ser dotado, como se hizo anteriormente, de una estructura de autómata finito. Si aquí se declara como finales a las clases [11] y [0011] entonces el autómata resultante será uno finito que reconoce al mismo lenguaje que el autómata no-determinista. Esta propiedad de ser equivalente a uno finito no es exclusiva del autómata en este ejemplo según veremos en el lema (3.3.2) más abajo.




Siguiente: Indeterminismo y determinismo
Un nivel arriba: Autómatas no-deterministas
Anterior: Representación de transiciones mediante
Guillermo Morales-Luna
2000-06-27
