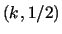 reversible one dimensional cellular automata
reversible one dimensional cellular automata
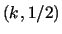 reversible one dimensional cellular automata
reversible one dimensional cellular automata
We can use transitions among block permutations to find periodical orbits in
![]() reversible one dimensional cellular automata. Take the set
reversible one dimensional cellular automata. Take the set ![]() formed with all the sequences of
formed with all the sequences of ![]() cells, with these sequences we can form
cells, with these sequences we can form ![]() configurations, each one of them obtained with the succesive repetition of one sequence in the set
configurations, each one of them obtained with the succesive repetition of one sequence in the set ![]() . In this way, for a configuration of this kind, we can know which is its succesor configuraton using the block permutations.
. In this way, for a configuration of this kind, we can know which is its succesor configuraton using the block permutations.
For
![]() , every configuration
, every configuration ![]() has the form
has the form
![]() for
for
![]() and every
and every ![]() maps to an unique block with the form
maps to an unique block with the form ![]() for
for ![]() and
and ![]() , then the whole configuration
, then the whole configuration ![]() maps to a sequence of blocks with the form
maps to a sequence of blocks with the form
![]() . Thus, we have only two kind of blocks,
. Thus, we have only two kind of blocks, ![]() and
and ![]() , and applying the permutation
, and applying the permutation ![]() , the block
, the block ![]() maps to an unique sequence
maps to an unique sequence
![]() . Making twice this process we have a mapping from the block
. Making twice this process we have a mapping from the block ![]() to another block
to another block ![]() placed in the same coordinates in relation to the positions in the configuration
placed in the same coordinates in relation to the positions in the configuration ![]() , this is showed in Figure 10.
, this is showed in Figure 10.
Applying the previous process to all the ![]() configurations, then we have a bijective mapping among the blocks
configurations, then we have a bijective mapping among the blocks ![]() because the cellular automaton is reversible, so every block has one ancestor and successor. With this, we can form a connectivity relation whose indices are blocks with the form
because the cellular automaton is reversible, so every block has one ancestor and successor. With this, we can form a connectivity relation whose indices are blocks with the form ![]() and the elements show the mapping from one block to another.
cr
and the elements show the mapping from one block to another.
cr
tc
We can define an equivalence relation in the connectivity relation defined in Table 1. If the block ![]() maps to
maps to ![]() and this block maps to
and this block maps to ![]() , then there is a mapping from
, then there is a mapping from ![]() to
to ![]() . We can do the transitive closure of the connectivity relation (for example, using the Warshall algorithm), and get the equivalence relation. Due to the periodical behavior of
. We can do the transitive closure of the connectivity relation (for example, using the Warshall algorithm), and get the equivalence relation. Due to the periodical behavior of
![]() reversible one dimensional cellular automata, every block
reversible one dimensional cellular automata, every block ![]() returns to itself and the transitive closure is also reflexive. If there exists a mapping from the block
returns to itself and the transitive closure is also reflexive. If there exists a mapping from the block ![]() to the block
to the block ![]() , then due also to the periodical behavior, there exists a mapping from
, then due also to the periodical behavior, there exists a mapping from ![]() to
to ![]() , thus the relation is symmetric and we have an equivalence relation, as is presented in Figure 11. Every class in this equivalence relation represents a set of periodic configurations. The period of every class is the number of elements that it has.
, thus the relation is symmetric and we have an equivalence relation, as is presented in Figure 11. Every class in this equivalence relation represents a set of periodic configurations. The period of every class is the number of elements that it has.
![\includegraphics[width=4in]{imagenes/equivalencia}](img134.gif)
|