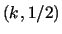 reversible one dimensional cellular automata
reversible one dimensional cellular automata
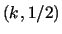 reversible one dimensional cellular automata
reversible one dimensional cellular automata
In the paper of Hedlund [Hed69], section 7 is devoted to analyse the dynamical behavior of the shift systems; based on his work we will do an analysis of periodic orbits in
![]() reversible one dimensional cellular automata.
reversible one dimensional cellular automata.
Suppose that a given configuration ![]() in the configuration set
in the configuration set ![]() is formed by the successive repetition of a finite sequence
is formed by the successive repetition of a finite sequence ![]() of
of ![]() cells. Thus, the states that form this configuration have a period
cells. Thus, the states that form this configuration have a period ![]() . Now, suppose that we apply an invertible evolution rule
. Now, suppose that we apply an invertible evolution rule ![]() , since the action of this rule is a block permutation, we can characterize the periodical behavior under the global mapping
, since the action of this rule is a block permutation, we can characterize the periodical behavior under the global mapping ![]() induced by
induced by ![]() of a configuration
of a configuration ![]() formed by a periodical finite sequence
formed by a periodical finite sequence
![]() .
.
Since all the sequences of length ![]() cells are in the finite set
cells are in the finite set ![]() , and the cardinality of the set
, and the cardinality of the set ![]() is
is
![]() , then in some moment during the evolution of the automaton we have to repeat the same sequence
, then in some moment during the evolution of the automaton we have to repeat the same sequence ![]() . Thus, the maximum period of the configuration
. Thus, the maximum period of the configuration ![]() formed with the repetition of a finite sequence
formed with the repetition of a finite sequence ![]() of length
of length ![]() is
is ![]() .
.
![]()
In the general case of
![]() reversible one dimensional cellular automata, Theorem 1 defines a maximum period of
reversible one dimensional cellular automata, Theorem 1 defines a maximum period of ![]() steps; where
steps; where ![]() is the neighborhood radius and
is the neighborhood radius and ![]() is the length of the finite sequence
is the length of the finite sequence ![]() whose repetition forms the configuration
whose repetition forms the configuration ![]() . We have to point out that this maximum period in most cases is a bad quote, because the practical experience shows that this period is much smaller.
. We have to point out that this maximum period in most cases is a bad quote, because the practical experience shows that this period is much smaller.
Periodic orbits
![]() of period
of period ![]() goes from a centered cylinder set to the same cilinder set. Since every sequence
goes from a centered cylinder set to the same cilinder set. Since every sequence ![]() of length
of length ![]() cells defines a centered cylinder set, then the family of all centered cilinder sets forms a finite covering of the configuration space
cells defines a centered cylinder set, then the family of all centered cilinder sets forms a finite covering of the configuration space
![]() . Then, a consequence of Theorem 1 and using Definition 6 is the following:
. Then, a consequence of Theorem 1 and using Definition 6 is the following:
Now we will use block permutations for detecting the periodical behavior of these systems.