Mean field probabilities

  

Figure: Mean field probabilities seem to converge to 60% which favors the T3 triangles.

A good place to begin the analysis of a cellular automaton is to consider its statistical behavior, insofar as it can be deduced from the rule of evolution.

For Rule 110, the table of evolution is

$$\begin{array}{\vert c\vert c\vert c\vert c\vert c\vert c\vert... ...hline 0 & 1 & 1 & 1 & 0 & 1 & 1 & 0 \\ \hline \end{array}$$

with the boolean formula

$$\begin{eqnarray*}\varphi(a,b,c) = b \oplus c \oplus abc \end{eqnarray*}$$

given states a, b, c in three successive cells. According to the table. Langton's parameter for the automaton is $\lambda =5/8$, or 0.625. The self-consistent mean field probability is given by p & = & 2pq² + 3p²q

whose positive root is p = 0.612 (the golden ratio) which, like Langton's parameter, requires slightly more than half of the cells to be alive.

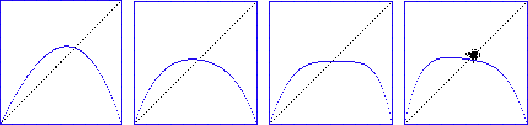
Figure 11 shows the mean field curves for four successive generations of evolution. Superposed on the last curve are 200 Monte Carlo points which shows that actual experience, at least in fhe first generations, favors a value intermediate between Langton's value, the mean field value, and the a priori value of 50%, but in the vicintiy of all of them.

Constructing the evolution is a kind of tiling problem [90] for the plane, or at least a half-plane. But given the variety and specific shapes of the tiles it does not fit into one of the traditional categories. As a dissection problem it is akin to squaring the square or triangling the triangle [95].

Again, observation of evolution from random initial configurations shows a marked preference for T3 triangles (this nomenclature reflects the number of zero cells on the top line, or on the left edge, of the triangle). It is possible to tile the plane with triangles of any size, but for larger triangles some mixtures are needed.

There are two enantiomorphic tilings of the plane using T3 triangles exclusively, but one of them does not interact well with the rule forbidding prolongations of top edges (concretely, they are incompatible with $\varphi(1,1,1)=0$). Cook called the other tiling the ether.

A reason for the predominance of the ether can probably be seen in the mean field probabilities, once the ratio of ones to zeroes in the individual tiles is examined.

  

Figure: A T5 tile, illustrating triangles' canonical shape and from which the relative proportion of zeroes and ones may be deduced. Left: T5 decorated according to evolution in Rule 110. Right: An unadorned plane-tiling S5.

Figure 12 shows a T5 tile, which is typical of all of them. To minimize overlapping and get a good tiling exercise, the right margin and the bottom margin are left off the tile, since they will always be provided by the abutting tile. Some additional overlap is inevitable since a neighboring triangle making contact along the hypotenuse always intersects the hypotenuse.

For plane tiling purposes, it is better to invent T0 triangles consisting of a single cell, and leave the diagonal off Tn triangles altogether. The new style can be called Sn, and by avoiding questions of overlap, give a more classical tiling exercise. In either event, we can elaborate the following table:

$$\begin{array}{lll} {\rm statistic} & {\rm Tn} & {\rm Sn} \\... ...portion\ of\ ones} & 6/(n+7) & (4n+2)(n^2+5n+2) . \end{array}$$

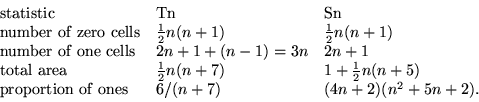
From this table it can already be seen that large triangles are at a disadvantage, although the disadvantage only obeys a 1/n law, and that there is an optimal approach to the mean field value at n=3. The following table describes this trend for Tn:

$$\begin{array}{\vert c\vert\vert c\vert c\vert c\vert c\vert c... ...75 & 0.35 & 0.33 & 0.26 & 0.30 & 0.28 \\ \hline \end{array}$$

If one confides in mean field theory at the 10% level, T1 is really out of range, T2 is not much better, nor are T5 nor anything further along the sequence. It is not excluded that some T2-T5 mixtures could be concocted, and it is seen that the hypotenusal overlaps won't affect the statistics much.

For reference, the absolute sizes of the first Tn's are shown in the following table.

$$\begin{array}{\vert c\vert c\vert\vert c\vert c\vert c\vert c... ...53 & 64 & 76 & 89 & 103 & 118 & 134 \\ \hline \end{array}$$

The main purpose of listing the areas of these tiles lies in the packing problem which arises when the unit cell of a glider wants to be filled. Certain areas are available as cells, which are to be packed with tiles. The number of tiles is the total amount of diagonal available, and the S₀'s are not freely available. Due to the prohibition against extending top edges, they can only occur singly, on diagonals. Furthermore, they occupy alternate diagonal sites, so that in the end roughly half the diagonal space availlable in a cell is dedicated to S₀'s.

It is possible to speculate whether the properties of the mean field theory curves favor the T3 gliders, or whether the predominasnce of T3 gliders in later generations moved the mean field equilibrium. At least in the first few generations, where the influence of correlations is presumably smaller than in the later generations, both tiny and large triangles are at a disadvantage, it is still possible to feel that T3's are statistical favorites.