![]()
Wolfram sugiere una clasificación de los autómatas celulares por las características presentadas en la evolución. El observó que los autómatas celulares tienden a caer en las siguientes clases:
1) La evolución es guiada hacia sistemas homogéneos.
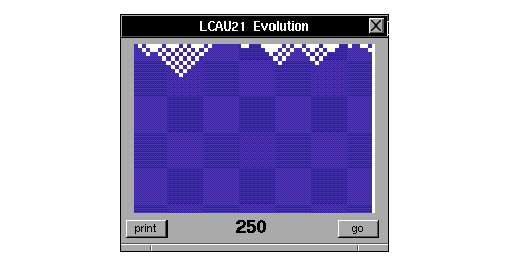
Figure 1.2: Ejemplo de la clase I en un autómata 21.
2) La evolución es guiada hacia un conjunto separado de estados estables o estructuras periódicas.

Figure 1.3: Ejemplo de la clase II en un autómata 21
3) La evolución es guiada a patrones caóticos
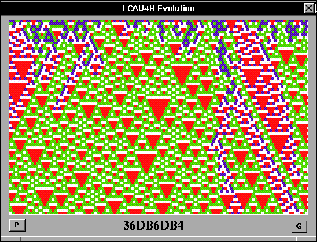
Figure 1.4: Ejemplo de la clase III em un autómata 4H
4) La evolución es guiada a complejas estructuras localizadas que algunas veces sobreviven.
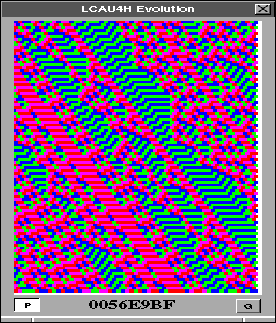
Figure 1.5: Ejemplo de la clase IV en un autómata 4H
Los autómatas celulares totalísticos son usados como ejemplo de estas 4 clases, para uno de ellos, K denota el número de estados por ejemplo: S = { 0 , 1 , . . , K-1} y r denota el número de radio de la vecindad, por ejemplo N = { -k, . . , 0 , . . r }. Cuando k=2 y r=2 (dos estados por celda y una vecindad de 5), hay 264) reglas totalísticas, asumiendo que la configuración en la cual todos los ceros, corta este número a la mitad. Estas reglas son etiquetadas por una función la cual es un número binario.
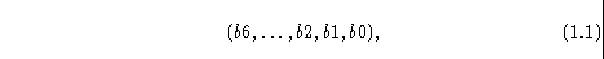
para
![]()
se interpreta que:
![]()
Usualmente esta función binaria es convertida a números decimales por conveniencia.
La restricción para el caso donde el cero o estado tranquilo está compuesto, significa
que todas las reglas consideradas tienen siempre números entre 0 y 62. Wolfram considero
todas las reglas con k=2 y r=2 , él las clasificó en las siguientes:
![]()