![]()
El trabajo de Moore [5] (1962), sobre la existencia
del Jardín del Edén probó que si existen configuraciones que no tuvieran ningún
ancestro, entonces debían existir configuraciones que tuvieran más de uno; durante este
tiempo los matemáticos profesionales no se interesaban en el desarrollo de AC, por lo que
el estudio de la reversibilidad permaneció estancado; catorce años después, los
resultados del trabajo de Toffoli [6] probaron la
existencia de ACLR que podían ser relevantes para el modelado de fenómenos físicos.
Independientemente Fredkin [7] había estado
estudiando la invertibilidad de modelos con comportamiento dinámico y desarrolló
técnicas para sintetizar un comportamiento secuencial arbitrario reversible con funciones
booleanas.
Uno de los objetivos de la ciencia de la computación es obtener modelos abstractos de
computadoras concretas, es decir, cualquier aparato computador que puede ser construido
fisicamente. En estos modelos uno busca expresividad (que el modelo capture todos los
aspectos relevantes de la computadora), y exactitud (que el modelo realize computaciones
correctas). Los Autómatas Celulares Lineales Reversibles (ACLR), son un importante
desarrollo en esa dirección de significancia comparable a la máquina de Turing [8]. Los AC son más expresivos que las máquinas de
Turing, ya que nos dan una manera explícita de modelar computación en paralelo, sin
embargo, ambas clases de modelos son indiferentes a un aspecto fundamental de la física,
la reversibilidad y así visualizar la posibilidad de una computación perpetua. En
general, los ACLR proveen un modelado más exacto y productivo para estos fines, hace unos
pocos años lo que se conocía acerca de ACLR era escaso y poco interesante, sin embargo,
actualmente ha alcanzado un mayor desarrollo. Los campos que trabajan actualmente con ACLR
incluyen: computación concurrente en redes que tienen estructura uniforme, preservación
de información en procesos computacionales, encontrar conexiones fundamentales entre la
física y la computación, computación cuántica, fundamentos de la relatividad, modelado
de sistemas físicos granulares, mayor calidad en la simulación de AC y encriptación de
datos.
Un AC es un sistema determinístico, es decir, para cada posible configuración su
regla de evolución especifica un sólo sucesor, existen ACL en los que podemos encontrar
una nueva regla que oblige al autómata a invertir su evolución en el tiempo. Por
supuesto, esto es sólo posible si la regla de evolución es determinística hacia atrás,
como lo señalan Toffoli y Margolus [6], es decir, si
para cada posible configuración existe uno y sólo un ancestro, a este tipo de ACL se les
denomina reversibles, en estos ACLR se pueden observar dos importantes propiedades:
a) Suryectividad, se define un ACL como suryectivo si cada configuración tiene
al menos un ancestro.
b) Inyectividad, un ACL es inyectivo si cada una de sus configuraciones tiene a
lo más un ancestro.
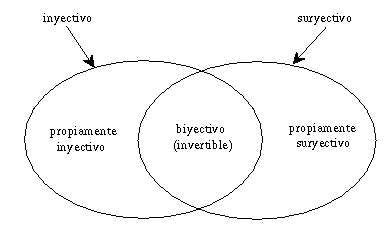
Si ambas propiedades se cumplen para un ACL se dice que es biyectivo o reversible.
El siguiente diagrama de Venn definido por Toffoli y Margolus (Gutowitz [7]), ilustra estas propiedades.
La regla que hace que el sistema regrese en el tiempo, es decir, la reversible a la
regla de evolución original se denomina regla inversa, en la mayoría de los casos la
regla inversa es diferente de la original; finalmente, excepto para el caso de un ACL no
se conoce un procedimiento sistemático para decidir cuando o no un AC es reversible.
![]()
Seck Tuoh Mora Juan Carlos
E-mail:seck@delta.cs.cinvestav.mx