![]()
Primero. Autómata (2,1), regla 85.
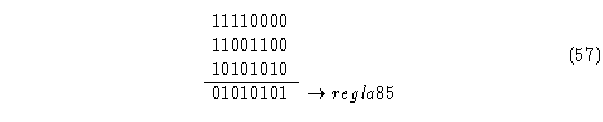
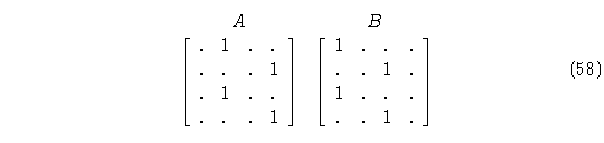
Matrices de conectividad A y B del diagrama de de Bruijn.
Matriz de evolución.
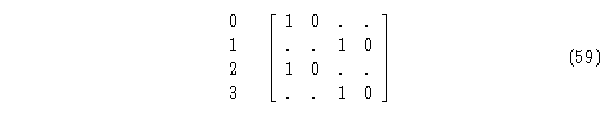
Estas matrices de conectividad son estocásticas por renglón, veamos su diagrama de
Parejas.
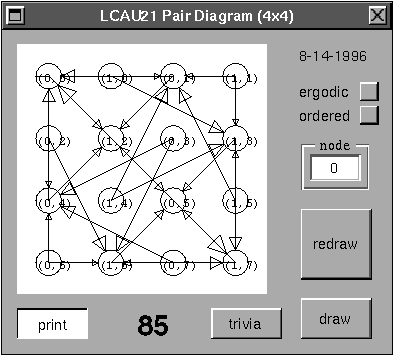
Se observa que no existen ciclos fuera de la diagonal, lo cual es una condición necesaria más no suficiente para que este autómata sea reversible, dada una configuración aleatoria se verá como evoluciona para obtener la evolución hacia atrás en el tiempo de cada posible vecindad.
Como se nota en este fragmento de evolución, las vecindades evolucionan hacia atrás,
en un único elemento.
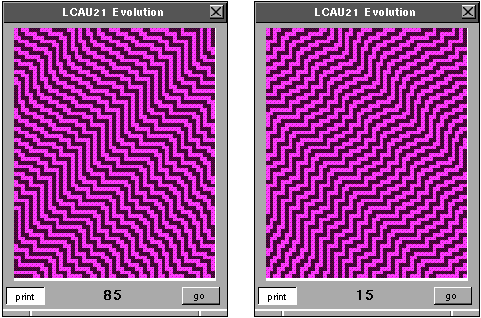
Autómata (2,1) regla 85 y su regla inversa 15. Segundo. Autómata (4,h), regla 0055AAFF.
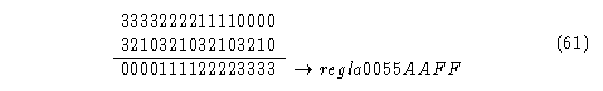
Matrices de conectividad A, B, C y D del diagrama de de Bruijn.
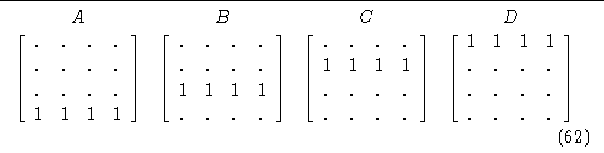
Matriz de Evolución.
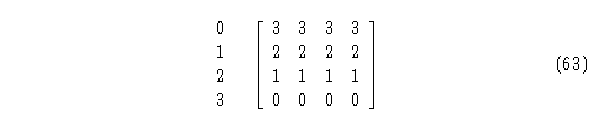
Veamos el diagrama de Parejas.
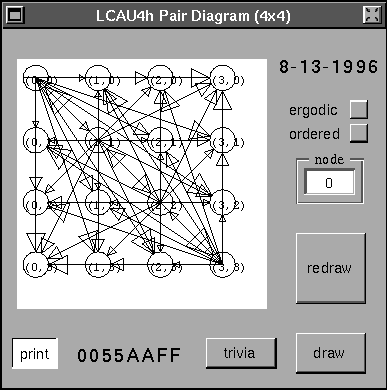
También se ve que no existen ciclos fuera de la diagonal, dada una configuración
aleatoria se analizará su evolución.

En estas evoluciones también se puede observar que las vecindades evolucionan hacia
atrás en un único elemento.

Autómata (4,h) regla 0055AAFF y su regla inversa 1B1B1B1B.
Seck Tuoh Mora Juan Carlos
E-mail:seck@delta.cs.cinvestav.mx