![]()
Primero. Autómata (2,1), regla 90.
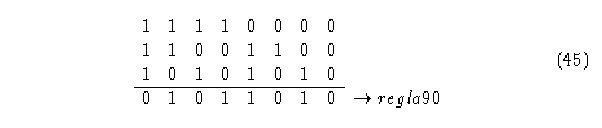
Matrices de conectividad.
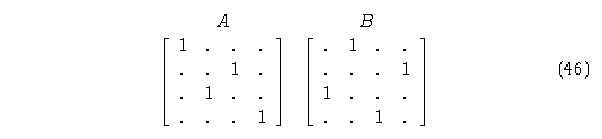
Se observa que las matrices de conectividad son estocásticas por renglón y por columna, que representan a la matriz de evolución.
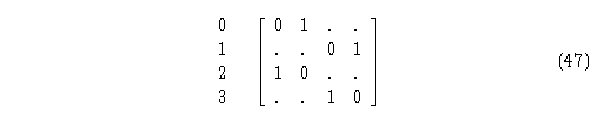
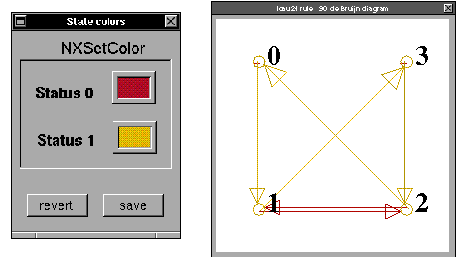
Veamos el diagrama de Parejas.
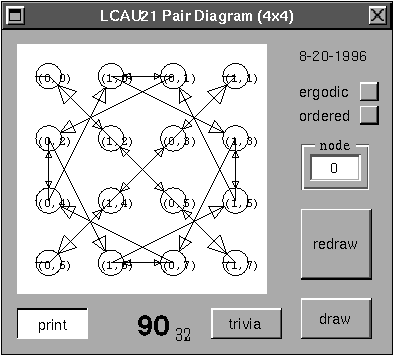
Como se puede observar en el diagrama de parejas, existen ciclos fuera de la diagonal,
lo que indica que algunas configuraciones tienen múltiples ancestros.
Tomemos la siguiente secuencia de nodos:
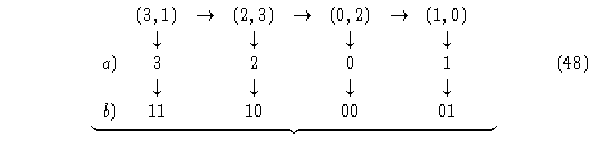
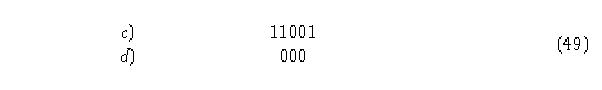
a) Elementos i (izquierdos) de cada nodo.
b) Nodos del diagrama de de Bruijn.
c) Configuración en el tiempo t.
d) Evolución en el tiempo t+1.
La configuración 000 evoluciona en el pasado en el estado 0, tomemos ahora los elementos j (derechos):
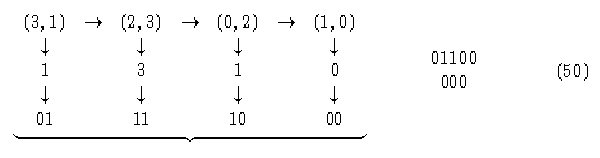
La configuración 000 evoluciona en el pasado en el estado 1, por lo tanto, este
autómata presenta múltiples ancestros, así como ciclos fuera de la diagonal en el
diagrama de parejas y consecuentemente no es reversible.

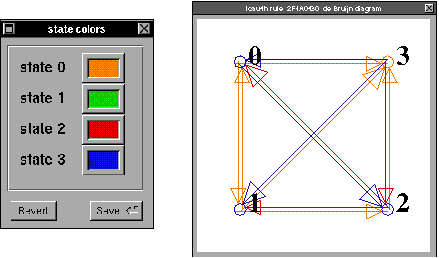
Segundo. Autómata (4,h), regla 2F1A0430.
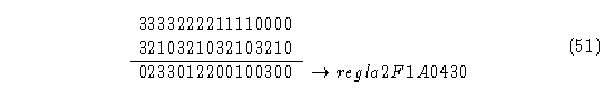
Matrices de conectividad A, B, C y D del diagrama de de Bruijn.
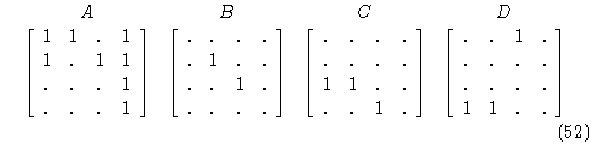
Matriz de evolución.
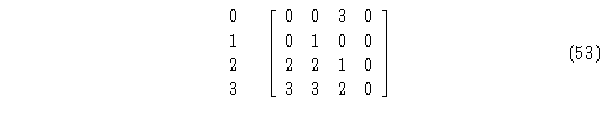
Veamos su diagrama de Parejas.
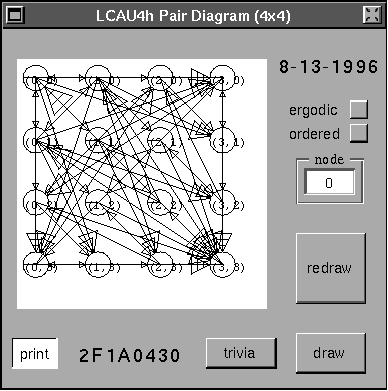
En este diagrama también existen ciclos fuera de la diagonal, indicando que existen
configuraciones que tienen múltiples ancestros.
Tomemos la siguiente secuencia de nodos:
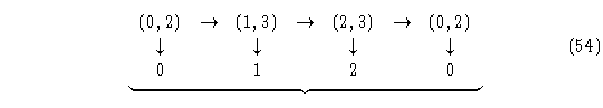
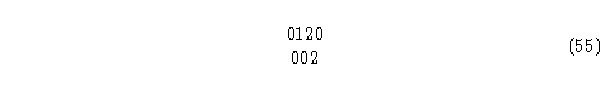
trabajando con los elementos i (izquierdos), la configuración 02 evoluciona en el pasado, en el estado 2, observando ahora los elementos j (derechos):
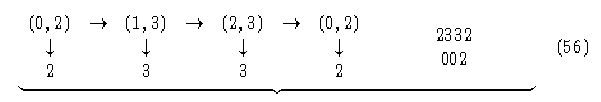
la configuración 02 evoluciona en el pasado, en el estado 3, por lo tanto, tiene más
de un ancestro.

Seck Tuoh Mora Juan Carlos
E-mail:seck@delta.cs.cinvestav.mx