![]()
El enfoque "inverso" es el que históricamente dió origen a los Autómatas
celulares, von Neumann estaba buscando un modelo para un fin en especial y así fue como
surgió el A.C., otro de los autómatas celulares célebres que fue creado bajo esta
línea de estudio es el juego de la vida de Conway[2].
El ejemplo que se muestra sobre esta línea es la construcción de un A.C. para un fin
muy específico: Un contador binario.
Como hacer que la información viaje a través de un A.C., a pesar de que la localidad
de las interacciones es parte de lo que se va a ilustrar la construcción del contador
binario.
De hecho se puede ver no solamente como la información viaja, sino como se construye
toda una maquinaria que interactúa: la expansividad, la existencia de "gliders"
(configuraciones que viajan), "still life" (configuraciones que se conservan
durante la evolución) son ejemplos de todas las características que estan directamente
relacionadas con la regla de transacción.
Una especificación más detallada se encuentra en[4],
aquí se muestra una de las maneras de construirlo, y se recrea aprovechando las
facilidades que NXLCAU ofrece.
Un contador binario es un incremento de uno sobre una base de dos números: 0 y 1
. Si uno incrementa en 1 el valor de 0 este se convertirá en 1 , y
no habrá acarreo. Si por otro lado se incrementa el 1 en 1 el valor será 10
, es decir 0 y se lleva 1 en el acarreo.
Entonces para construir un contador binario mediante un A.C. se deben hacer las siguientes consideraciones:
Son en total cuatro estados los que se necesitan para este tipo de contador, por lo que
usaremos el A.C. (4,1).
Una característica más que tendrá nuestro contador es un lanzador de incrementos, que envia constantemente el incremento a 1 para que interactúen sobre los estados 0 y 1 .
Consideremos también la siguiente tabla de equivalencia entre estados y colores:
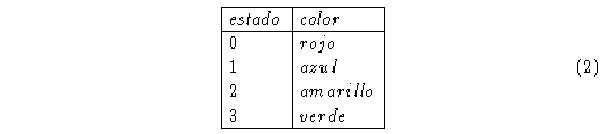
A continuación comenzamos a construir el contador binario:
![]()