Siguiente: En campos finitos Un nivel arriba: El-Gamal Anterior: El-Gamal

En anillos de residuos

Recordamos que si p es un número primo, entonces $Z\!\!\!Z_p$ es un campo, y su grupo multiplicativo $Z\!\!\!Z_p^*=Z\!\!\!Z_p-\{0\}$ es un grupo cíclico. Cada generador de $Z\!\!\!Z_p^*$ es un elemento primitivo en $Z\!\!\!Z_p^*$. Si x es un elemento primitivo, entonces

$$\forall y\in Z\!\!\!Z_p^*\exists!z\in[\![0,p-2]\!]:\ x^z=y\mbox{\rm mod }p$$

tal z es el logaritmo discreto de y en base x, en $Z\!\!\!Z_p^*$. Escribimos, $z=\log_x(y)$.

En la tabla 3.1 vemos que 14 es primitivo en $Z\!\!\!Z_{17}^*$ así como todas sus potencias impares (esto porque 17-1=16 es una potencia de 2), a saber: 14, 7, 12, 6, 3, 10, 5, 11.

  

Table: Potencias de 14 módulo 17 y logaritmos discretos en base 14 en $Z\!\!\!Z_{17}^*$.

En esa misma tabla, observamos que la inversa de la función ``potencia de 14'', a saber el logaritmo discreto en base 14, tiene un comportamiento que parece aleatorio. La función exponenciación es relativamente sencilla: Si $k=\sum_i a_i 2^i$ entonces

$$x^k=\prod_i \left(x^{a_i}\right)^{2^i}=\prod_{\{i\vert a_i=1\}} x^{2^i}.$$

Ahora bien, si se define la sucesión $\left(x_i\right)_i$ como

$$x_0=x \hspace{3em},\hspace{3em} x_i=x_{i-1} x_{i-1}$$

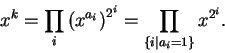
entonces x²ⁱ=x_i. Sin embargo, el cálculo de logaritmos discretos es un problema completo-NP. En este sentido es que la exponenciación es una función unidireccional.

El Método de ElGamal se resume como sigue:

Espacio de llaves.

${\cal L}=\{(p,x,z,y)\vert x^z=y\mbox{\rm mod }p\}$. En cada cuarteta $(p,x,z,y)\in {\cal L}$ la terceta e=(p,x,y) es la llave pública y d=z es la llave secreta.

Procedimiento de encriptamiento.

Es no-determinista. Dado $m\in Z\!\!\!Z_p^*$, elíjase aleatoriamente $k\in Z\!\!\!Z_p^*$ y hágase

$$c=f(m,k)=\left(x^k\mbox{\rm mod }p,m\cdot y^k\mbox{\rm mod }p\right).$$

Procedimiento de desencriptamiento.

Dado c=(v₁,v₂), y conocida la llave secreta d=z hágase

$$g(v_1,v_2)=v_2\left(v_1^z\right)^{-1}\mbox{\rm mod }p.$$

El procedimiento es correcto pues si se tuviera

$$c=(v_1,v_2)=\left(x^k\mbox{\rm mod }p,m\cdot y^k\mbox{\rm mod }p\right)$$

entonces

$$v_1^z = \left(x^k\right)^z\mbox{\rm mod }p = y^k\mbox{\rm mod }p$$

y, en consecuencia,

$$v_2\left(v_1^z\right)^{-1}\mbox{\rm mod }p=m\cdot y^k\cdot y^{-k}\mbox{\rm mod }p = m.$$

Ejemplo: Supongamos elegido el primo p=1438033, el cual es el 109789-ésimo primo. Entonces $p-1=1438032=2^4\cdot 3\cdot 29959$.

Consideremos el elemento primitivo $x= 278783= 17\cdot 23^2\cdot 31$. Y como llave secreta el exponente z = 45276. Entonces $y=x^z\mbox{\rm mod }p=1153553$. La llave pública es pues (p,x,y)=(1438033, 278783, 1153553).

Ahora, si alguien quiere enviar un mensaje, digamos m= 89279, entonces genera un número aleatorio $k\in[\![0,p-2]\!]$, digamos k=1376276. Calcula

$$\begin{eqnarray*}v_1 &=& \hspace{1em}\ \; x^k\mbox{\rm mod }p= 1435954 \\ v_2 &=& m\cdot y^k\mbox{\rm mod }p= 502371 \end{eqnarray*}$$

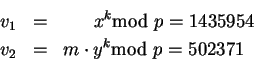
El cifrado es pues c=(v₁,v₂)=(1435954, 502371).

Ahora, partiendo de c, con la llave secreta z se calcula $w_1= v_1^z\mbox{\rm mod }p= 748458$. Su inverso multiplicativo en $Z\!\!\!Z_p$ es w₁^-1= 1015266. Así pues el producto

$$m'=v_2 w_1^{-1}\mbox{\rm mod }p =502371\cdot 1015266\mbox{\rm mod }1438033= 89279=m$$

efectivamente coincide con m.

 

La seguridad del método de ElGamal se basa en la dificultad del Problema del logaritmo discreto:


Instancia:

Solución:

Siguiente: En campos finitos Un nivel arriba: El-Gamal Anterior: El-Gamal