


Posterior: Homomorfismos
Arriba: Filtros y homomorfismos
Anterior: Filtros y homomorfismos
Sea
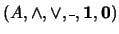 un álgebra booleana.
un álgebra booleana.
Definición 4.1
Un
FILTRO es un conjunto

que cumple las implicaciones siguientes:
De manera dual, un
IDEAL es un conjunto
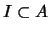
que cumple las implicaciones siguientes:
Así por ejemplo, si  es un elemento arbitrario, su cono superior
es un elemento arbitrario, su cono superior
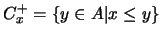 es un filtro de
es un filtro de  , llamado FILTRO PRINCIPAL GENERADO POR
, llamado FILTRO PRINCIPAL GENERADO POR  y su cono inferior
y su cono inferior
 es un ideal de
es un ideal de  , llamado IDEAL PRINCIPAL GENERADO POR
, llamado IDEAL PRINCIPAL GENERADO POR  . Para
. Para
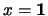 , el filtro principal que genera consta únicamente de
, el filtro principal que genera consta únicamente de 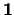 , en tanto que el ideal principal que genera es toda el álgebra
, en tanto que el ideal principal que genera es toda el álgebra  . Para
. Para 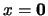 , el ideal principal que genera consta únicamente de
, el ideal principal que genera consta únicamente de  , en tanto que el filtro principal que genera es toda el álgebra
, en tanto que el filtro principal que genera es toda el álgebra  . Un ideal o un filtro es PROPIO si es distinto de los casos extremos:
. Un ideal o un filtro es PROPIO si es distinto de los casos extremos:
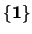 y
y  en el caso de filtros y
en el caso de filtros y
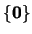 y
y  en el caso de ideales.
El álgebra booleana
en el caso de ideales.
El álgebra booleana  se dice ser de IDEALES PRINCIPALES si todo ideal es un ideal principal generado por algún elemento en
se dice ser de IDEALES PRINCIPALES si todo ideal es un ideal principal generado por algún elemento en  . Si
. Si  es un álgebra finita, entonces ciertamente es de ideales principales.
es un álgebra finita, entonces ciertamente es de ideales principales.
Definición 4.2
Un conjunto
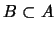
se dice tener la
PROPIEDAD DE INTERSECCIÓN FINITA si todo conjunto finito de

tiene un ínfimo no-nulo:
Para un conjunto  , sea
, sea 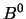 el conjunto de elementos minorizados por algún elemento en
el conjunto de elementos minorizados por algún elemento en  :
:
y sea  el conjunto de ínfimos de conjuntos finitos en
el conjunto de ínfimos de conjuntos finitos en  :
:
Una BASE de un filtro  es todo conjunto
es todo conjunto  tal que
tal que  . Una SUB-BASE del filtro
. Una SUB-BASE del filtro  es un conjunto
es un conjunto  tal que
tal que  sea una base de
sea una base de  .
.
Demostración
Observamos primeramente que para cada  :
:
De aquí resulta claro que
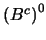 es, en efecto, un filtro.
Ahora, si
es, en efecto, un filtro.
Ahora, si  es un filtro que contiene a
es un filtro que contiene a  , entonces claramente
, entonces claramente 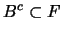 y también
y también
 .
Para probar el último punto, observamos que si acaso
.
Para probar el último punto, observamos que si acaso  no tuviese la propiedad de intersección finita, entonces existirían
no tuviese la propiedad de intersección finita, entonces existirían
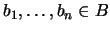 tales que
tales que
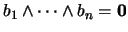 . Por tanto
. Por tanto
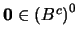 y, en consecuencia,
y, en consecuencia,
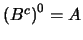 . Así pues,
. Así pues,
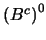 no es propio. Recíprocamente, si
no es propio. Recíprocamente, si
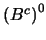 no fuese propio, entonces
no fuese propio, entonces
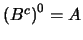 y habría
y habría
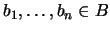 tales que
tales que
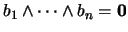 , es decir,
, es decir,  no tendría la propiedad de intersección finita.
no tendría la propiedad de intersección finita.  Un filtro es un subconjunto de un álgebra booleana. Por tanto, la colección de filtros propios forma un conjunto ordenada con la relación de ``contención de conjuntos''. Los elementos maximales en esa colección son los ultrafiltros.
Un filtro es un subconjunto de un álgebra booleana. Por tanto, la colección de filtros propios forma un conjunto ordenada con la relación de ``contención de conjuntos''. Los elementos maximales en esa colección son los ultrafiltros.
Definición 4.3
Un filtro propio
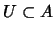
es un
ULTRAFILTRO si para todo filtro

rige la implicación:
Una primera caracterización de ultrafiltros la da la proposición siguiente:
Proposición 4.2
Un filtro propio
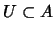
es un ultrafiltro si y sólo si se cumple la condición:
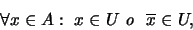 |
(1) |
es decir, para todo elemento en el álgebra, bien él o su complemento, mas no ambos, está en el ultrafiltro.
Demostración
Supongamos primero que  sea un ultrafiltro. Sea
sea un ultrafiltro. Sea  un elemento tal que
un elemento tal que 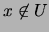 . Sea
. Sea 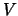 el filtro generado por
el filtro generado por 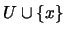 . Al ser
. Al ser  un ultrafiltro contenido propiamente en
un ultrafiltro contenido propiamente en 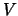 necesariamente
necesariamente 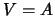 . Por tanto
. Por tanto 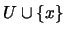 no tiene la propiedad de intersección finita. Así, existen
no tiene la propiedad de intersección finita. Así, existen
 tales que
tales que
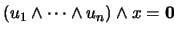 , es decir
, es decir
 , o sea
, o sea
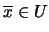 .
.
Recíprocamente, supongamos que se cumple la condición (1). Sea  un filtro cualquiera que contenga propiamente a
un filtro cualquiera que contenga propiamente a  . Entonces para algún
. Entonces para algún  se tiene
se tiene 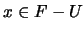 . Por (1) se ha de tener que
. Por (1) se ha de tener que
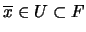 . Así pues, ambos elementos
. Así pues, ambos elementos  y
y 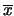 están en
están en  y, en consecuencia,
y, en consecuencia,
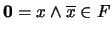 . Por tanto
. Por tanto  no puede ser propio pues ha de coincidir con
no puede ser propio pues ha de coincidir con  . Así pues,
. Así pues,  no puede estar contenido propiamente en un filtro propio y, en consecuencia,
no puede estar contenido propiamente en un filtro propio y, en consecuencia,  es un ultrafiltro.
es un ultrafiltro.  Por ejemplo, si
Por ejemplo, si 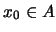 es un átomo en el álgebra booleana, entonces su cono superior
es un átomo en el álgebra booleana, entonces su cono superior  es un ultrafiltro.
En efecto, veamos que se cumple la condición (1). Sea
es un ultrafiltro.
En efecto, veamos que se cumple la condición (1). Sea  tal que
tal que 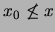 . Entonces
. Entonces
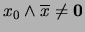 . Al ser
. Al ser 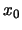 un átomo, necesariamente
un átomo, necesariamente
 , es decir
, es decir
 , lo cual indica que
, lo cual indica que
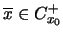 .
En general, aún en álgebras que no sean atómicas, se tiene que habrá ultrafiltros. De hecho, cualquier filtro queda contenido en algún ultrafiltro.
.
En general, aún en álgebras que no sean atómicas, se tiene que habrá ultrafiltros. De hecho, cualquier filtro queda contenido en algún ultrafiltro.
Teorema 4.1 (de ultrafiltros)
Todo filtro en un álgebra booleana puede extenderse a un ultrafiltro.
Demostración
Sea  un filtro en un álgebra booleana y sea
un filtro en un álgebra booleana y sea  la colección de filtros que contienen a
la colección de filtros que contienen a  .
.  no es vacío pues
no es vacío pues 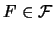 .
.  está ordenado por inclusión. Un ultrafiltro será un elemento maximal en
está ordenado por inclusión. Un ultrafiltro será un elemento maximal en  . Para ver que existen elementos maximales utilizaremos el Lema de Zorn: Si en un conjunto ordenado toda cadena está acotada superiormente, entonces existen elementos maximales.
Sea pues
. Para ver que existen elementos maximales utilizaremos el Lema de Zorn: Si en un conjunto ordenado toda cadena está acotada superiormente, entonces existen elementos maximales.
Sea pues
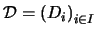 una cadena en
una cadena en  , y sea
, y sea
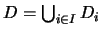 . Veamos que
. Veamos que 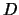 es un filtro:
Si
es un filtro:
Si  entonces existen
entonces existen 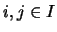 tales que
tales que 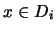 e
e  . Al ser
. Al ser  una cadena, para algún
una cadena, para algún  se ha de tener que
se ha de tener que 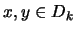 . Como
. Como 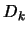 es un filtro,
es un filtro,
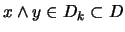 .
Si
.
Si 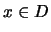 y
y  entonces para alguna
entonces para alguna 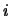 ,
, 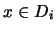 y al ser éste un filtro,
y al ser éste un filtro,
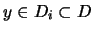 .
Ahora bien, como para todo
.
Ahora bien, como para todo 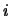 ,
,
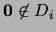 , se tiene que
, se tiene que
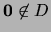 .
.
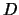 es pues un filtro propio que acota superiormente a la cadena
es pues un filtro propio que acota superiormente a la cadena  .
Así pues,
.
Así pues,  posee elementos maximales. Cualquiera de éstos es un ultrafiltro que extiende al filtro
posee elementos maximales. Cualquiera de éstos es un ultrafiltro que extiende al filtro  .
. 
Observación 4.1
Cualquier conjunto de elementos en un álgebra booleana que tenga la propiedad de intersección finita puede extenderse a un ultrafiltro.
En efecto, todo conjunto con la propiedad de intersección finita se extiende a un filtro y éste a su vez a un ultrfiltro.
Observación 4.2
Todo elemento no-nulo en un álgebra booleana está contenido en un ultrafiltro.
En efecto, si  es tal que
es tal que
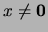 entonces la mónada
entonces la mónada 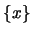 tiene la propiedad de intersección finita. Por tanto se extiende a un ultrafiltro.
tiene la propiedad de intersección finita. Por tanto se extiende a un ultrafiltro.
Observación 4.3
Dados dos elementos cualesquiera en un álgebra booleana, existe un ultrafiltro que los separa, es decir:

, si
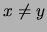
entonces existe un ultrafiltro

tal que
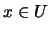
pero
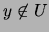
.
En efecto, si 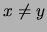 entonces bien
entonces bien 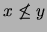 o
o 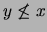 . Supongamos
. Supongamos 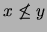 , entonces
, entonces
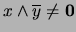 . Así pues, la pareja
. Así pues, la pareja
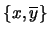 tiene la propiedad de intersección finita. Por tanto se extiende a un ultrafiltro, digamos
tiene la propiedad de intersección finita. Por tanto se extiende a un ultrafiltro, digamos  . Pues bien,
. Pues bien, 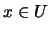 y, como
y, como
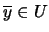 ,
, 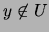 .
. 
Observación 4.4
Si
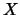
es un conjunto infinito, entonces el álgebra booleana de sus partes,
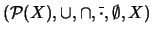
posee un ultrafiltro no-principal.
En efecto, sea
 la colección de conjuntos cofinitos en
la colección de conjuntos cofinitos en 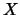 . Entonces
. Entonces
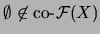 y cualesquiera dos elementos en
y cualesquiera dos elementos en
 se cortan. Estas dos propiedades bastan para ver que
se cortan. Estas dos propiedades bastan para ver que
 tiene la propiedad de intersección finita. Un ultrafiltro que lo extienda no puede ser principal.
tiene la propiedad de intersección finita. Un ultrafiltro que lo extienda no puede ser principal. 



Posterior: Homomorfismos
Arriba: Filtros y homomorfismos
Anterior: Filtros y homomorfismos
Guillermo Morales-Luna
2004-07-27