

Posterior: Geometría de Lobachevski
Arriba: Geometría del espacio
Anterior: Geometría del espacio
Sea
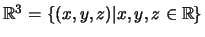 el espacio real de tres dimensiones.
Dados
el espacio real de tres dimensiones.
Dados
 y
y
 , la recta algebraica que pasa por
, la recta algebraica que pasa por
 y tiene VECTOR DIRECTOR
y tiene VECTOR DIRECTOR
 es el conjunto
es el conjunto
Naturalmente, vale la equivalencia:
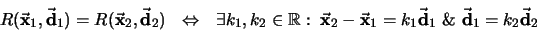 |
(5) |
en otras palabras, dos rectas coinciden si el segmento que une a los puntos por donde pasan y los dos vectores directores son todos paralelos. Como criterio de pertenencia de un punto a una recta se tiene:

Dados
 y
y
 , el plano algebraico que pasa por
, el plano algebraico que pasa por
 y tiene VECTOR NORMAL
y tiene VECTOR NORMAL
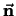 es el conjunto
es el conjunto
donde
es el producto ``interno'', o ``punto'', usual.
Naturalmente, vale la equivalencia:
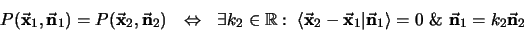 |
(7) |
en otras palabras, dos planos coinciden si los dos vectores normales son paralelos y el segmento que une a los puntos por donde pasan es ortogonal a ellos. Como criterio de pertenencia de un punto a un plano se tiene:

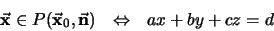 |
(8) |
donde
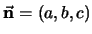 y
y
 .
Al conjunto de rectas algebraicas lo reducimos mediante la relación de equivalencia dada por (5), y a cada clase de equivalencia la llamamos RECTA GEOMÉTRICA. Similarmente, al conjunto de planos algebraicos lo reducimos mediante la relación de equivalencia dada por (7), y a cada clase de equivalencia la llamamos PLANO GEOMÉTRICO. Evidentemente, los criterios de pertenencia dados por (6) y (8) son congruentes con (5) y (7) respectivamente.
La colección de puntos, rectas geométricas y planos geométricos constituyen naturalmente una
.
Al conjunto de rectas algebraicas lo reducimos mediante la relación de equivalencia dada por (5), y a cada clase de equivalencia la llamamos RECTA GEOMÉTRICA. Similarmente, al conjunto de planos algebraicos lo reducimos mediante la relación de equivalencia dada por (7), y a cada clase de equivalencia la llamamos PLANO GEOMÉTRICO. Evidentemente, los criterios de pertenencia dados por (6) y (8) son congruentes con (5) y (7) respectivamente.
La colección de puntos, rectas geométricas y planos geométricos constituyen naturalmente una
 -estructura en donde se cumplen todos los axiomas de Hilbert. Esta estructura se dice ser EUCLIDIANA.
-estructura en donde se cumplen todos los axiomas de Hilbert. Esta estructura se dice ser EUCLIDIANA.


Posterior: Geometría de Lobachevski
Arriba: Geometría del espacio
Anterior: Geometría del espacio
Guillermo Morales-Luna
2004-07-27