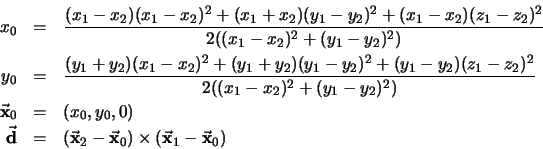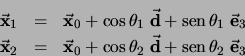

Posterior: Plano de Fano
Arriba: Geometría del espacio
Anterior: Geometría analítica
Sea
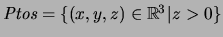 el ``semiespacio superior abierto por debajo'' en el espacio real de tres dimensiones.
Sea
el ``semiespacio superior abierto por debajo'' en el espacio real de tres dimensiones.
Sea
 la ``tapa de abajo'' del conjunto
la ``tapa de abajo'' del conjunto
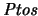 .
Para
.
Para
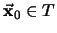 y
y
 sea
sea
 el semicírculo con centro en
el semicírculo con centro en
 y ``radio principal''
y ``radio principal''
 , ortogonal a
, ortogonal a 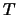 . Entonces,
. Entonces,
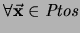 :
:
donde
 .
Sea también
.
Sea también
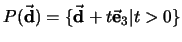 la recta perpendicular a
la recta perpendicular a 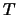 que pasa por
que pasa por
 .
El conjunto de ``rectas'' es
.
El conjunto de ``rectas'' es
Ahora, para
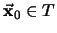 y
y 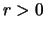 , sea
, sea
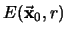 la semiesfera con centro en
la semiesfera con centro en
 y radio
y radio 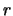 , ``ortogonal'' a
, ``ortogonal'' a 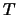 :
:
donde
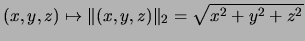 es la, así llamada, NORMA EUCLIDIANA. También, para cada
es la, así llamada, NORMA EUCLIDIANA. También, para cada
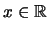 y
y ![$t\in]0,2\pi[$](img498.png) sea
sea
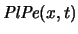 el plano que es perpendicular al plano
el plano que es perpendicular al plano 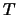 , corta al eje de las
, corta al eje de las 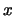 's en el punto
's en el punto 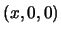 y forma un ángulo de
y forma un ángulo de 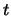 radianes con el eje de las
radianes con el eje de las 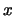 's. Sea, finalmente,
's. Sea, finalmente, 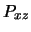 el plano de coordenadas que contiene a los ejes de las
el plano de coordenadas que contiene a los ejes de las 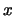 's y los
's y los 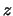 's.
El conjunto de ``planos'' es
's.
El conjunto de ``planos'' es
La unión de conjuntos
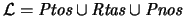 , llamada GEOMETR´iA DE LOBACHEVSKI, forma una
, llamada GEOMETR´iA DE LOBACHEVSKI, forma una
 -estructura. De hecho, las relaciones unarias, binarias y terciarias de
-estructura. De hecho, las relaciones unarias, binarias y terciarias de
 se interpretan naturalmente en
se interpretan naturalmente en 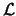 . Las relaciones cuaternarias, de congruencia, principalmente, han de interpretarse viendo la ``congruencia'' de segmentos mediante alguna proyección hiperbólica: Mientras más cercano se esté al plano
. Las relaciones cuaternarias, de congruencia, principalmente, han de interpretarse viendo la ``congruencia'' de segmentos mediante alguna proyección hiperbólica: Mientras más cercano se esté al plano 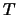 , las distancias deben ser mayores. Tan solo para hacer un poco más explícitos los comentarios anteriores observemos lo siguiente:
Si
, las distancias deben ser mayores. Tan solo para hacer un poco más explícitos los comentarios anteriores observemos lo siguiente:
Si
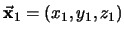 ,
,
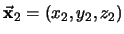 son dos puntos tales que la recta euclidiana que los une no es perpendicular a
son dos puntos tales que la recta euclidiana que los une no es perpendicular a 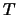 , entonces
, entonces
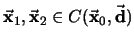 donde
donde
Entonces existirán dos ángulos
![$\theta_1,\theta_2\in]0,\pi[$](img510.png) tales que
tales que
y la distancia entre
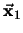 y
y
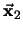 será
será
En este modelo se cumplen también todos los axiomas de Hilbert. Sin embargo, en él no se cumple el axioma de las paralelas. Dada una recta y un punto que no esté en ella es posible encontrar una infinidad de rectas que están en el plano que contiene al punto y a la recta dados, que pasan por el punto pero no cortan a la recta. En otras palabras,, por un punto fuera de una recta se puede hacer pasar una infinidad de rectas paralelas a la dada.
Así pues, el axioma de las paralelas es independiente de los demás axiomas de la Geometría de Hilbert.
Ahora bien, la Geometría de Lobachevski la hemos construído partiendo del modelo euclidiano de la Geometría Analítica que sí satisface el axioma de las paralelas. De manera general podemos resumir esto, diciendo que si la geometría euclidiana es consistente entonces la geometría no-euclidiana también lo será.


Posterior: Plano de Fano
Arriba: Geometría del espacio
Anterior: Geometría analítica
Guillermo Morales-Luna
2004-07-27