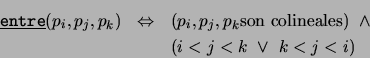Posterior: Deducción natural en el
Arriba: Geometría del espacio
Anterior: Geometría de Lobachevski
En este ejemplo presentaremos un modelo de geometrías finitas en el plano. En él interpretaremos sólo las nociones de
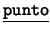 y
y
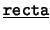 y a las relaciones que las involucran.
Consideraremos un conjunto de siete rectas y un conjunto de siete puntos. La relación
y a las relaciones que las involucran.
Consideraremos un conjunto de siete rectas y un conjunto de siete puntos. La relación
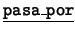 la interpretamos como una del conjunto de rectas al conjunto de puntos. Sea
la interpretamos como una del conjunto de rectas al conjunto de puntos. Sea
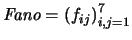 la matriz tal que
la matriz tal que
Explícitamente, hemos de tener:
Puede verse fácilmente que siempre es posible encontrar una recta única que pase por dos puntos dados, cada recta contiene al menos dos puntos y existe una tríada (de hecho hay
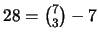 ) de puntos no colineales. Así que se cumplen inmediatamente los tres primeros axiomas de incidencia de la Geometría de Hilbert.
Ahora, interpretemos a la relación
) de puntos no colineales. Así que se cumplen inmediatamente los tres primeros axiomas de incidencia de la Geometría de Hilbert.
Ahora, interpretemos a la relación
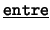 como sigue:
como sigue:
Resulta con esto, que si una recta ``entra'' a un triángulo por un lado, entonces ha de ``salir'' por uno de los otros dos lados. En consecuencia, este modelo satisface los axiomas primero, tercero y cuarto de orden. Deja de cumplir con el segundo pues siendo éste un modelo finito, no puede ocurrir que entre cualesquiera dos puntos exista un tercero entre ellos.



Posterior: Deducción natural en el
Arriba: Geometría del espacio
Anterior: Geometría de Lobachevski
Guillermo Morales-Luna
2004-07-27


![\begin{displaymath}\mbox{\it Fano}=\left[\begin{array}{ccccccc}
1 & 0 & 0 & 1 &...
... 0 & 0 \\
0 & 1 & 1 & 0 & 0 & 0 & 1 %%\\
\end{array}\right]\end{displaymath}](img520.png)