

Posterior: Silogística
Arriba: Cálculo de predicados
Anterior: Plano de Fano
Sea 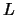 un lenguaje apropiado para una teoría de primer orden. Sea
un lenguaje apropiado para una teoría de primer orden. Sea
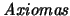 el conjunto de axiomas lógicos, de reescritura y extralógicos. Hemos visto que éstos últimos son los que caracterizan a una teoría.
El cálculo de predicados sobre
el conjunto de axiomas lógicos, de reescritura y extralógicos. Hemos visto que éstos últimos son los que caracterizan a una teoría.
El cálculo de predicados sobre 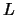 consta de las fórmulas bien formadas que se pueden deducir del conjunto de axiomas. El procedimiento de deducción, al igual que en el cálculo de proposiciones, queda determinado por las reglas de inferencia.
consta de las fórmulas bien formadas que se pueden deducir del conjunto de axiomas. El procedimiento de deducción, al igual que en el cálculo de proposiciones, queda determinado por las reglas de inferencia.
La primera regla de inferencia no requiere comentarios pues ya la hemos
utilizado en este curso. La segunda formaliza el conocido procedimiento para
demostrar una proposición cuantificada universalmente: Se considera un
elemento cualquiera 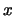 y se ve que vale
y se ve que vale 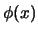 , luego, dado que
, luego, dado que 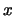 es
arbitrario, se concluye que, en efecto,
es
arbitrario, se concluye que, en efecto, 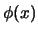 vale para cualquier
vale para cualquier 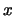 .
.
Definición 3.2 (Pruebas)
Sea
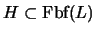
una colección de fórmulas bien formadas sobre el lenguaje
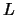
, llamadas
hipótesis. Una
PRUEBA es una sucesión finita
![$D=[\phi_1,\ldots,\phi_n]$](img528.png)
de fórmulas bien formadas tal que
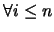
:
En este caso la prueba
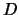
se dice ser una
prueba de 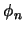 a partir de
a partir de 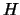
. Se escribe
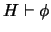
para denotar el hecho de que

es
DEMOSTRABLE, es decir, que existe una prueba de
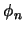
a partir de
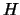
.
El conjunto de fórmulas
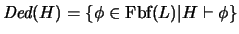
consta de todas las fórmulas demostrables a partir de
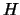
. Éste se dice ser la
TEOR´i
A de
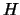
.
Se observa inmediatamente que vale una especie de transitividad en la noción de demostrabilidad:
Proposición 3.1
Sean
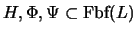
tres conjuntos de fórmulas y sean
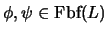
otras dos fórmulas. Entonces vale la siguiente implicación:
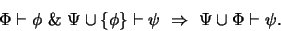 |
(3) |
En consecuencia, el ``operador''
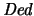 es un operador de cerradura: Para cualesquiera
es un operador de cerradura: Para cualesquiera
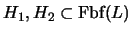 :
:
-
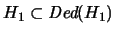 .
.
-
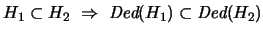 .
.
-
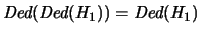 .
.
Definición 3.3
El conjunto de
TEOREMAS en
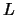
es
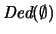
, es decir, es el conjunto de fórmulas demostrables partiendo únicamente de los axiomas. El conjunto de teoremas se dice ser también la
TEOR´i
A DE PRIMER ORDEN resultante del lenguaje
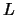
con los
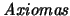
.
Ejemplo 3.1
Sea
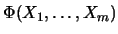
una tautología del cálculo proposicional. Si
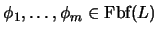
son
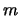
fórmulas bien formadas, entonces al sustituir cada variable proposicional

por la fórmula
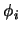
se obtiene la fórmula
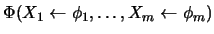
que es una
TAUTOLOG´i
A del cálculo de predicados.
Se tiene que
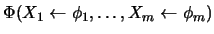
es un teorema.
En efecto, al ser
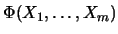 una tautología, por el Teorema de Completitud del cálculo proposicional, es también un teorema, es decir, existe una demostración de
una tautología, por el Teorema de Completitud del cálculo proposicional, es también un teorema, es decir, existe una demostración de
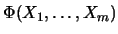 . Esta es evidentemente también una demostración de
. Esta es evidentemente también una demostración de
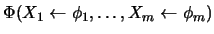 en el cálculo de predicados.
en el cálculo de predicados. 
Ejemplo 3.2
Para cada

se tiene
es decir, cuantificadores universales consecutivos pueden intercambiarse.
Demostración
Una prueba es la siguiente:
- 1.
-
 (
(
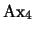 )
)
- 2.
-
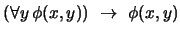 (
(
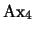 )
)
- 3.
-
![$\begin{array}[t]{l}
\left(\left(\forall y\, \phi(x,y)\right)\ \rightarrow\ \ph...
...\forall y\, \phi(x,y)\right)\ \rightarrow\ \phi(x,y)\right)\right)
\end{array}$](img558.png) (
(
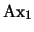 )
)
- 4.
-
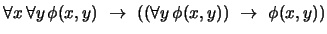 (
(
 )
)
- 5.
-
![$\begin{array}[t]{l}
\left(\forall x\, \forall y\, \phi(x,y)\ \rightarrow\ \lef...
...ll x\, \forall y\, \phi(x,y)\ \rightarrow\ \phi(x,y)\right)\right)
\end{array}$](img562.png) (
(
 )
)
- 6.
-
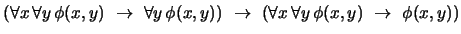 (
(
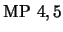 )
)
- 7.
-
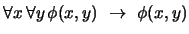 (
(
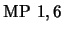 )
)
- 8.
-
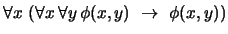 (
(
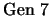 )
)
- 9.
-
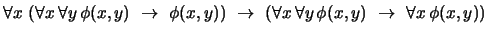 (
(
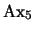 )
)
- 10.
-
 (
(
 )
)
- 11.
-
 (
(
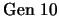 )
)
- 12.
-
![$\begin{array}[t]{l}
\forall y\, \left(\forall x\, \forall y\, \phi(x,y)\ \righ...
..., \phi(x,y)\ \rightarrow\ \forall y\, \forall x\, \phi(x,y)\right)
\end{array}$](img576.png) (
(
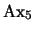 )
)
- 13.
-
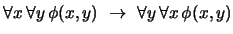 (
(
 )
)

Ejemplo 3.3
Para cada

se tiene
es decir, ``un predicado que no es simétrico para ninguna pareja no puede cortar a la diagonal''.
Demostración
Escribiremos una prueba de ese teorema. Para simplificar la escritura mínimamente, abreviaremos
En la tabla 3.4 presentamos esa prueba.
Table 3.4:
Prueba de
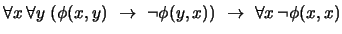 .
.
![\begin{table}
\begin{quote}\begin{enumerate}\item[1.] $\Phi\ \rightarrow\ \fora...
...,x)$\ \hfill ($\mbox{\rm MP}\ 20,21$)
\end{enumerate}\end{quote}
\end{table}](img581.png) |
 Así como en el cálculo proposicional el Teorema de la Deducción proporciona un procedimiento para simplificar demostraciones, en el cálculo de predicados se tiene también una propia versión de este teorema para facilitar pruebas. Sólo que aquí, debido al uso de variables, hay que proceder con un mayor cuidado para enunciar y demostrar ese teorema.
En efecto, obsérvese que para una fórmula con una sola variable libre
Así como en el cálculo proposicional el Teorema de la Deducción proporciona un procedimiento para simplificar demostraciones, en el cálculo de predicados se tiene también una propia versión de este teorema para facilitar pruebas. Sólo que aquí, debido al uso de variables, hay que proceder con un mayor cuidado para enunciar y demostrar ese teorema.
En efecto, obsérvese que para una fórmula con una sola variable libre
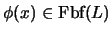 , por la regla de generalización se tiene
, por la regla de generalización se tiene
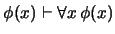 , sin embargo, no es cierto que
, sin embargo, no es cierto que
 , pues en esta última fórmula, la primera aparición de
, pues en esta última fórmula, la primera aparición de 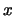 se refiere a un término en particular, no a un elemento genérico. Es decir, una variable libre
se refiere a un término en particular, no a un elemento genérico. Es decir, una variable libre 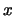 a la izquierda del símbolo
a la izquierda del símbolo 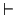 se refiere a un objeto sintáctico arbitrario que aún no se ha evaluado, en tanto que la misma variable libre
se refiere a un objeto sintáctico arbitrario que aún no se ha evaluado, en tanto que la misma variable libre 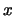 a la derecha de
a la derecha de 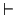 se refiere a un término que en cualquier interpretación ha de tener una correspondiente evaluación. De este ejemplo, se ve que es precisamente en la aplicación de la regla de generalización que hay que poner especial atención al enunciar el correspondiente teorema de la Deducción.
se refiere a un término que en cualquier interpretación ha de tener una correspondiente evaluación. De este ejemplo, se ve que es precisamente en la aplicación de la regla de generalización que hay que poner especial atención al enunciar el correspondiente teorema de la Deducción.
Definición 3.4
Sea
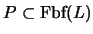
un conjunto de fórmulas bien formadas,

una fórmula en
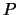
y sea
![$\left[\phi_1,\ldots,\phi_m\right]$](img589.png)
una prueba construída a partir de
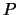
. Se dice que
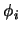 DEPENDE
DEPENDE de

si se cumple alguna de las proposiciones siguientes:
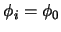
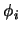 se sigue de alguna fórmula que depende de
se sigue de alguna fórmula que depende de  .
.
Resulta claro que si 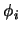 no depende de
no depende de  , entonces vale la implicación:
, entonces vale la implicación:
 |
(4) |
Teorema 3.1 (de la Deducción)
Sea
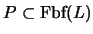
un conjunto de fórmulas bien formadas y sean
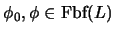
dos fórmulas. Supongamos que
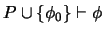
y que existe una prueba de esto en la que la regla de generalización no se haya aplicado a ninguna fórmula que dependa de

, respecto a una variable libre de

. Entonces
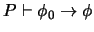
.
El recíproco del Teorema de Deducción,
es válido como una consecuencia de la regla Modus Ponens.
Demostración
Sea
![$\left[\phi_1,\ldots,\phi_n=\phi\right]$](img597.png) una prueba de
una prueba de  construída a partir de
construída a partir de
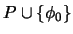 . Probemos por inducción en
. Probemos por inducción en 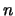 que
que
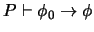 .
Caso base. Supongamos
.
Caso base. Supongamos 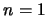 . Entonces
. Entonces
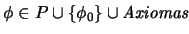 .
Si
.
Si 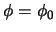 entonces, al ser
entonces, al ser
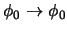 un teorema lógico,
un teorema lógico,
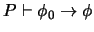 .
En otro caso, una prueba de
.
En otro caso, una prueba de
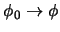 es:
es:
- 1.
-
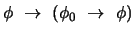 (
(
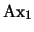 )
)
- 2.
 (
(
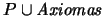 )
)
- 3.
-
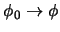 (
(
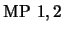 )
)
Caso inductivo. Supongamos 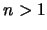 y que el teorema se cumple para demostraciones de longitud estrictamente menor que
y que el teorema se cumple para demostraciones de longitud estrictamente menor que 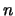 .
Ya que
.
Ya que
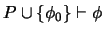 , puede ocurrir que
, puede ocurrir que
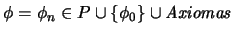 o bien que
o bien que 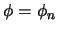 es el resultado de aplicar una de las dos reglas de inferencia a fórmulas anteriores en la prueba.
En el primer caso, como ya se vió en el caso base, se tiene
es el resultado de aplicar una de las dos reglas de inferencia a fórmulas anteriores en la prueba.
En el primer caso, como ya se vió en el caso base, se tiene
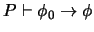 .
En el segundo caso, hay que ver cuál es la regla de inferencia que le dió lugar.
.
En el segundo caso, hay que ver cuál es la regla de inferencia que le dió lugar.
Modus ponens. Para algunos índices anteriores  las correspondientes fórmulas han de ser de la forma
las correspondientes fórmulas han de ser de la forma
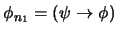 y
y
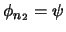 . Por la hipótesis de inducción se tiene que existe una prueba
. Por la hipótesis de inducción se tiene que existe una prueba 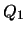 de que
de que
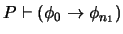 y una prueba
y una prueba 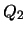 de que
de que
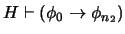 , digamos que de
, digamos que de 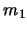 y
y 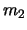 pasos. La concatenación de
pasos. La concatenación de 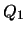 y
y 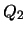 con los siguientes pasos da una prueba de
con los siguientes pasos da una prueba de
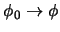 a partir de
a partir de 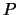 :
:
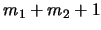 .
.-
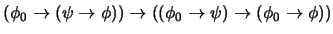 (
(
 )
)
 .
.-
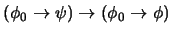 (
(
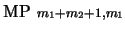 )
)
 .
.-
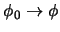 (
(
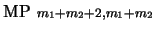 )
)
Generalización. Supongamos que para algna fórmula anterior  ,
, 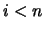 , se tiene
, se tiene
 . Por la hipótesis del teorema, se tiene que bien
. Por la hipótesis del teorema, se tiene que bien  no depende de
no depende de  o bien
o bien 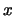 no aparece libre en
no aparece libre en  .
En el primer caso, por la relación (4), se tiene
.
En el primer caso, por la relación (4), se tiene
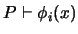 . Una prueba de esto último, digamos que de
. Una prueba de esto último, digamos que de 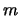 pasos, se extiende mediante los pasos siguientes a una prueba de
pasos, se extiende mediante los pasos siguientes a una prueba de
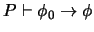 :
:
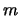 .
. (
(
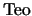 )
)
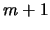 .
.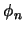 (
(
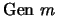 )
)
 .
.-
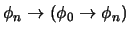 (
(
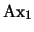 )
)
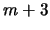 .
.-
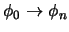 (
(
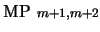 )
)
En el segundo caso, por la hipótesis de inducción se tiene
y una prueba de esto último, digamos que de 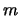 pasos, se extiende mediante los pasos siguientes a una prueba de
pasos, se extiende mediante los pasos siguientes a una prueba de
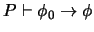 :
:
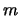 .
.-
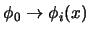 (
(
 )
)
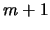 .
.-
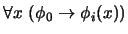 (
(
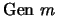 )
)
 .
.-
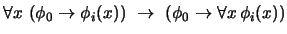 (
(
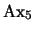 )
)
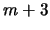 .
.-
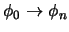 (
(
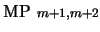 )
)
 En la siguiente subsección veremos que este cálculo de predicados contiene al clásico (en varios sentidos).
En la siguiente subsección veremos que este cálculo de predicados contiene al clásico (en varios sentidos).
Subsections


Posterior: Silogística
Arriba: Cálculo de predicados
Anterior: Plano de Fano
Guillermo Morales-Luna
2004-07-27
 ,
,  :
:
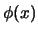 , donde
, donde 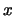 aparece
libre en
aparece
libre en  :
:
![$\begin{array}[t]{l}
\left(\left(\forall y\, \phi(x,y)\right)\ \rightarrow\ \ph...
...\forall y\, \phi(x,y)\right)\ \rightarrow\ \phi(x,y)\right)\right)
\end{array}$](img558.png) (
(
![$\begin{array}[t]{l}
\left(\forall x\, \forall y\, \phi(x,y)\ \rightarrow\ \lef...
...ll x\, \forall y\, \phi(x,y)\ \rightarrow\ \phi(x,y)\right)\right)
\end{array}$](img562.png) (
(
![$\begin{array}[t]{l}
\forall y\, \left(\forall x\, \forall y\, \phi(x,y)\ \righ...
..., \phi(x,y)\ \rightarrow\ \forall y\, \forall x\, \phi(x,y)\right)
\end{array}$](img576.png) (
(