


Posterior: Completitud
Arriba: Coherencia y completitud
Anterior: Coherencia
En el conjunto de fórmulas bien formadas
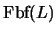 definamos la relación siguiente:
definamos la relación siguiente:
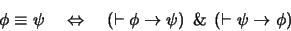 |
(1) |
Es claro que 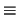 es una relación de equivalencia. El cociente
es una relación de equivalencia. El cociente
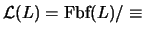 se dice ser el ´ALGEBRA DE LINDENBAUM del alfabeto
se dice ser el ´ALGEBRA DE LINDENBAUM del alfabeto 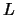 .
. 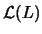 es, en efecto, un álgebra booleana con las operaciones inducidas por los conectivos lógicos en
es, en efecto, un álgebra booleana con las operaciones inducidas por los conectivos lógicos en
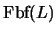 . El elemento máximo es la clase de equivalencia de los teoremas y el elemento mínimo la de las contradicciones. Más aún, el orden del álgebra queda caracterizado por la relación:
. El elemento máximo es la clase de equivalencia de los teoremas y el elemento mínimo la de las contradicciones. Más aún, el orden del álgebra queda caracterizado por la relación:
![\begin{displaymath}
{[\phi]} \leq [\psi] \ \ \ \Leftrightarrow\ \ \ \vdash \phi \rightarrow \psi
\end{displaymath}](img796.png) |
(2) |
Recordamos que si 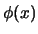 es una fórmula donde
es una fórmula donde  aparece libre (si apareciese también ligada entonces mediante un mero renombramiento de variables se deja en
aparece libre (si apareciese también ligada entonces mediante un mero renombramiento de variables se deja en 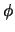 sólo las apariciones libres de la variable
sólo las apariciones libres de la variable  ), entonces
), entonces
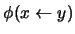 denota a la fórmula obtenida de sustituir toda aparición de
denota a la fórmula obtenida de sustituir toda aparición de  por la variable
por la variable 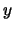 . Se tiene
. Se tiene
![\begin{displaymath}
{[\forall x\,\phi(x)]} = \bigwedge\left\{[\phi(x\leftarrow y)]\vert\, y\in\mbox{\rm Var}\right\}
\end{displaymath}](img798.png) |
(3) |
En efecto, por el axioma
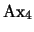 se tiene
se tiene
Por tanto
![${[\forall x\,\phi(x)]} \leq \bigwedge\left\{[\phi(x\leftarrow y)]\vert\, y\in\mbox{\rm Var}\right\}$](img800.png) .
Ahora, supongamos que la clase
.
Ahora, supongamos que la clase ![$[\psi]$](img801.png) sea una cota inferior de
sea una cota inferior de
![$\left\{[\phi(x\leftarrow y)]\vert\, y\in\mbox{\rm Var}\right\}$](img802.png) . Sea
. Sea 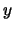 una variable que no aparezca en
una variable que no aparezca en 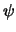 . Entonces hemos de tener
. Entonces hemos de tener
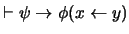 . Por Generalización se ha de tener también
. Por Generalización se ha de tener también
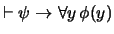 . Así pues,
. Así pues,
![$[\psi] \leq {[\forall x\,\phi(x)]}$](img805.png) .
.



Posterior: Completitud
Arriba: Coherencia y completitud
Anterior: Coherencia
Guillermo Morales-Luna
2004-07-27