Posterior: Coherencia Arriba: Cálculo de predicados Anterior: Formas clausulares

Coherencia y completitud

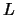Sea $L$ un alfabeto propio para una teoría de primer orden. Si 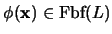$\phi(\mbox{\bf x})\in\mbox{\rm Fbf}(L)$ es una fórmula bien formada, en la que aparecen libres las variables 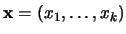$\mbox{\bf x}=(x_1,\ldots,x_k)$, la CERRADURA de 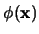$\phi(\mbox{\bf x})$ es el enunciado 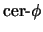$\mbox{\rm cer-}\phi$ que se obtiene al cuantificar de manera universal a las variables libres. De la regla de generalización y de los axiomas de tipo 4 se tiene

$$T\vdash \phi(\mbox{\bf x})\ \ \ \Leftrightarrow\ \ \ T\vdash \mbox{\rm cer-}\phi.$$