


Posterior: Ilustración del Teorema de
Arriba: El teorema de Goodstein
Anterior: Sucesión de Goodstein
Definimos a la función 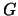 como
como
Puede probarse que la diagonal de 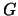 ``domina'' a cualquier función recursiva, es decir:
``domina'' a cualquier función recursiva, es decir:
con fines de la exposición aquí, y sin entrar en detalles técnicos, podemos pensar que las funciones recursivas son precisamente las funciones efectivamente computables.
Se tiene, en consecuencia, que:
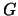 no puede ser recursiva y
no puede ser recursiva y
- el Teorema de Goodstein no es demostrable formalmente, pues
- una demostración formal de él daría un algoritmo para calcular
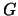 , y no puede existir tal algoritmo pues la función que calcularía tal algoritmo estaría acotada a la larga por
, y no puede existir tal algoritmo pues la función que calcularía tal algoritmo estaría acotada a la larga por 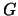 .
.
Guillermo Morales-Luna
2004-07-27