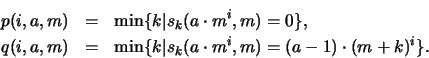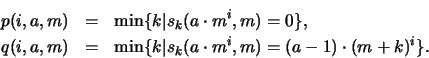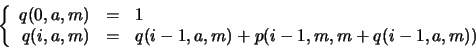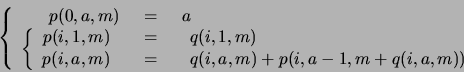Posterior: Resolución del sistema de
Arriba: El teorema de Goodstein
Anterior: Ilustración del Teorema de
Calcularemos valores para argumentos de la forma
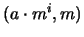 donde
donde
![$a\in[1,m-1],\;i\in[0,m-1]\mbox{\rm y }m\geq 2.$](img966.png) Definamos
Definamos
Entonces incialmente, para 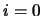 , se tiene
, se tiene 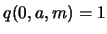 y
y 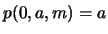 .
Recursivamente, para
.
Recursivamente, para 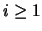 , los valores de
, los valores de 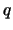 y de
y de 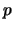 se calculan según los procedimientos descritos en los seudocódigos de la tabla 3.10.
se calculan según los procedimientos descritos en los seudocódigos de la tabla 3.10.
Table 3.10:
Cálculos de 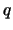 y de
y de 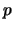 .
.
![\begin{table}
\begin{displaymath}\begin{array}{ll}
\fbox{
\begin{minipage}[t]...
... s$
\end{tabbing}
\end{minipage}
}
\end{array}\end{displaymath}
\end{table}](img972.png) |
Equivalentemente, se tiene las recurrencias siguientes:
y
De aquí se puede ver que 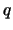 es ``constante respecto a
es ``constante respecto a 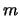 '',
'',
Guillermo Morales-Luna
2004-07-27