


Posterior: Campos de Galois
Arriba: Campos algebraicos
Anterior: Cuaterniones
Sea
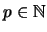 un número primo. La congruencia de enteros módulo
un número primo. La congruencia de enteros módulo 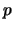 :
:
es una relación de equivalencia en los enteros 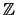 , congruente con las operaciones del anillo
, congruente con las operaciones del anillo 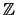 . Su espacio cociente
. Su espacio cociente
es entonces un anillo, llamado de los enteros módulo 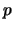 , con las operaciones heredadas de
, con las operaciones heredadas de 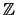 .
Al ser
.
Al ser 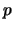 un primo, se tiene que para todo entero
un primo, se tiene que para todo entero 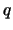 tal que
tal que 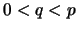 ,
, 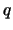 es primo relativo con
es primo relativo con 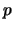 , por tanto el máximo común divisor de
, por tanto el máximo común divisor de 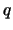 y
y 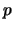 es 1,
es 1,
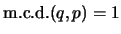 . Consecuentemente, 1 se ha de expresar como una combinación lineal de
. Consecuentemente, 1 se ha de expresar como una combinación lineal de 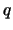 y
y 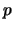 , es decir, existen
, es decir, existen
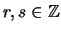 tales que
tales que 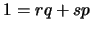 . Por tanto, al tomar congruencias móduo
. Por tanto, al tomar congruencias móduo 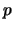 resulta
resulta
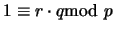 , vale decir,
, vale decir, 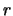 es el inverso multiplicativo de
es el inverso multiplicativo de 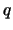 .
Así pues,
.
Así pues,
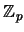 es un campo, finito, con
es un campo, finito, con 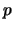 elementos, y por tanto una
elementos, y por tanto una
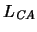 -estructura.
-estructura.
Guillermo Morales-Luna
2004-07-27