


Posterior: Algebras
booleanas Arriba: Campos
algebraicos Anterior: Enteros
módulo-
Sea 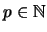 un
número primo.
un
número primo. 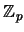 es un campo y la colección de polinomios
es un campo y la colección de polinomios ![${\mathbb{Z}}_p[X]$](img417.png) con coeficientes en él es un anillo.
Si
con coeficientes en él es un anillo.
Si 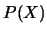 es un polinomio cualquiera de grado
es un polinomio cualquiera de grado 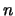 , el cociente
, el cociente ![${\mathbb{Z}}_p[X]/\left(P(X)\right)$](img419.png) es el introducido por la
relación de equivalencia de polinomios:
es el introducido por la
relación de equivalencia de polinomios:
y es un anillo con las operaciones heredadas de ![${\mathbb{Z}}_p[X]$](img417.png) . De hecho, puede verse que el cociente
. De hecho, puede verse que el cociente ![${\mathbb{Z}}_p[X]/\left(P(X)\right)$](img419.png) posee exactamente
posee exactamente 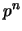 elementos. Si
elementos. Si 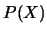 es además un polinomio
irreducible de grado
es además un polinomio
irreducible de grado 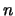 entonces el cociente
entonces el cociente ![${\mathbb{F}}_{p^n}={\mathbb{Z}}_p[X]/\left(P(X)\right)$](img422.png) es un
campo, llamado de Galois. Se puede ver que
es un
campo, llamado de Galois. Se puede ver que 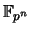 no depende del polinomio irreducible
no depende del polinomio irreducible 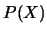 (si se toma algún otro polinomio irreducible
(si se toma algún otro polinomio irreducible 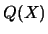 de grado
de grado 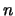 , el cociente
, el cociente ![${\mathbb{Z}}_p[X]/\left(Q(X)\right)$](img425.png) es isomorfo al cociente
es isomorfo al cociente ![${\mathbb{Z}}_p[X]/\left(P(X)\right)$](img419.png) ).
). 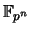 es un campo finito con
es un campo finito con 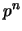 elementos, es cíclico y es de suma importancia en aplicaciones
relativas a las Telecomunicaciones, específicamente en la
Teoría de Códigos y en Criptografía. Todo esto se
puede ver con más detalle en los libros [Li] y [Sch].
elementos, es cíclico y es de suma importancia en aplicaciones
relativas a las Telecomunicaciones, específicamente en la
Teoría de Códigos y en Criptografía. Todo esto se
puede ver con más detalle en los libros [Li] y [Sch]. 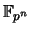 es pues una
es pues una 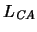 -estructura.
-estructura.



Posterior: Algebras
booleanas Arriba: Campos
algebraicos Anterior: Enteros
módulo-
Guillermo
Morales-Luna
2004-07-27