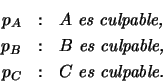

Posterior: Semánticas basadas en conjunción
Arriba: Lógicas proposicionales difusas
Anterior: Lógicas proposicionales difusas
Recordamos que un cálculo de proposiciones (CProp) se construye a
partir de un conjunto finito de variables proposicionales
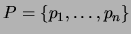 , de los valores constantes
, de los valores constantes 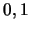 a los que se
identifica como falso y verdadero, respectivamente, y de
algunos conectivos, entre los cuáles están
a los que se
identifica como falso y verdadero, respectivamente, y de
algunos conectivos, entre los cuáles están
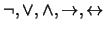 llamados negación,
disyunción, conjunción, implicación y equivalencia,
respectivamente. Las formas proposicionales son las así llamadas
fórmulas bien formadas. Para precisar el concepto de fórmula bien
formada asignemos primeramente prioridades a los conectivos:
llamados negación,
disyunción, conjunción, implicación y equivalencia,
respectivamente. Las formas proposicionales son las así llamadas
fórmulas bien formadas. Para precisar el concepto de fórmula bien
formada asignemos primeramente prioridades a los conectivos:
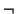 |
tiene prioridad |
1 |
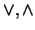 |
tienen
prioridad |
2 |
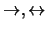 |
tienen prioridad |
2 |
En el manejo de prioridades, la convención es usual: ``Menores valores
numéricos corresponden a prioridades mayores y, con prioridades
iguales, se aplican primero los conectivos más a la izquierda''. El
conjunto FP de formas proposicionales se define inductivamente, y al
mismo tiempo se define la noción de conectivo principal de FP's.
En el recuadro (4.10) presentamos estas definiciones precisas.
Table 4.10:
Definición de formas proposicionales.
![\begin{table}\begin{center}\fbox{ \begin{minipage}[t]{35em} \begin{enumerate}
\...
...ay}\end{displaymath}\ \end{enumerate} \end{minipage}}\end{center}
\end{table}](img314.png) |
Por ejemplo, consideremos el acertijo siguiente:
Ha
ocurrido un cuantioso robo en una tienda. Los asaltantes transportaron su
botín en una camioneta. Posteriormente se atrapa a tres maleantes
sospechosos 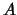 ,
, 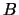 y
y 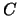 . Las pesquisas muestran evidencias de que
. Las pesquisas muestran evidencias de que 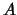 siempre se acompaña de
siempre se acompaña de 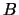 o de
o de 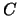 para sus fechorías,
para sus fechorías, 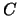 por su lado
nunca actuaría solo, pero también
por su lado
nunca actuaría solo, pero también 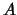 no se acompañaría de
no se acompañaría de 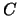 en
un atraco. El atraco sólo pudo haber sido cometido por
en
un atraco. El atraco sólo pudo haber sido cometido por 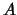 ,
, 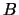 o
o 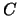 y
al menos uno de ellos es culpable.
Hay que decidir las culpabilidades de ellos.
y
al menos uno de ellos es culpable.
Hay que decidir las culpabilidades de ellos.
Consideremos tres variables proposicionales para codificar
correspondientes hipótesis:
Los ``hechos'' siguientes pueden
representarse por correspondientes formas proposicionales:
- Si
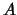 fuese culpable y
fuese culpable y 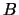 inocente,
entonces
inocente,
entonces 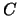 ha de ser culpable:
ha de ser culpable:
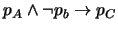 .
.
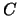 nunca actuaría solo:
nunca actuaría solo:
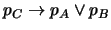 .
.
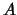 nunca actuaría con
nunca actuaría con 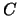 :
:
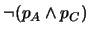 .
.
- Nadie más que
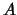 ,
, 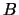 o
o 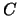 pudieron haber actuado y al menos uno
de ellos es culpable:
pudieron haber actuado y al menos uno
de ellos es culpable:
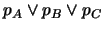 .
.
De acuerdo con el acertijo, si
los cuatro hechos anteriores fuesen verdaderos, ¿qué podría decirse
acerca de las culpabilidades de 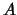 ,
, 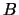 y
y 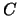 ? Y si acaso se tuviese una
evidencia de que cada uno de esos hechos es verdadero con una cierta
probabilidad, ¿qué podría decirse acerca de las probabilidades de
que
? Y si acaso se tuviese una
evidencia de que cada uno de esos hechos es verdadero con una cierta
probabilidad, ¿qué podría decirse acerca de las probabilidades de
que 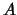 ,
, 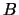 y
y 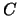 sean culpables?
El acertijo se formaliza naturalmente en un cálculo proposicional con tres variables.
En lo que sigue, trataremos el acertijo con las respectivas propagaciones de valores
que introduzcamos.
sean culpables?
El acertijo se formaliza naturalmente en un cálculo proposicional con tres variables.
En lo que sigue, trataremos el acertijo con las respectivas propagaciones de valores
que introduzcamos.


Posterior: Semánticas basadas en conjunción
Arriba: Lógicas proposicionales difusas
Anterior: Lógicas proposicionales difusas
Guillermo Morales-Luna
2004-07-28
,
y
. Las pesquisas muestran evidencias de que
siempre se acompaña de
o de
para sus fechorías,
por su lado nunca actuaría solo, pero también
no se acompañaría de
en un atraco. El atraco sólo pudo haber sido cometido por
,
o
y al menos uno de ellos es culpable. Hay que decidir las culpabilidades de ellos.