



Siguiente: Códigos de Reed-Muller
Arriba: Introducción a la Teoría
Anterior: Programas
Sea 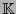 un campo finito y sea
un campo finito y sea
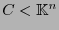 un código lineal-
un código lineal-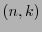 . Sea
. Sea
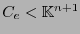 definido como sigue:
definido como sigue:
Naturalmente, 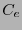 es un código lineal-
es un código lineal-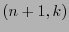 . Si
. Si
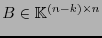 es una matriz revisora de paridad de
es una matriz revisora de paridad de  entonces una matriz revisora de paridad de
entonces una matriz revisora de paridad de 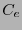 es
es
donde
 es el vector columna consistente de
es el vector columna consistente de 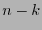 ceros y
ceros y
 es el vector renglón consistente de
es el vector renglón consistente de 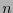 unos.
unos.
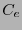 se dice ser el código extendido de
se dice ser el código extendido de  .
.
Observación 6.1
Si
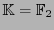 y
y
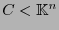 es un código lineal-
es un código lineal-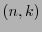 con peso mínimo
con peso mínimo 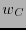 impar, entonces el peso mínimo de
impar, entonces el peso mínimo de 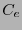 es
es 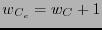 .
.
En efecto, si 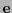 es de peso mínimo en
es de peso mínimo en  entonces el correspondiente vector
entonces el correspondiente vector  en
en 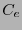 ha de ser tal que
ha de ser tal que  . Por tanto
. Por tanto
 .
. 
Observación 6.2
Para los códigos de Hamming 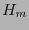 , de acuerdo con la observación 4.4, sus extendidos
, de acuerdo con la observación 4.4, sus extendidos 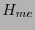 son de peso mínimo
son de peso mínimo 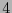 , y una matriz revisora de paridad de ellos es de la forma
, y una matriz revisora de paridad de ellos es de la forma
Sea
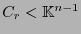 definido como sigue:
definido como sigue:
Si se escribe a una matriz revisora de paridad de  como
como
entonces una matriz revisora de paridad de 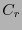 ha de ser
ha de ser
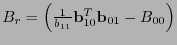 .
El código
.
El código 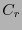 se dice ser recortado de
se dice ser recortado de  .
.
Observación 6.3
Un código es el recortado de su extendido y es también equivalente al extendido de su recortado.
Ahora, sea
 el espacio generado por
el espacio generado por  y la clase lateral
y la clase lateral  , donde
, donde 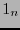 es el vector en
es el vector en  constante 1:
constante 1:
El código 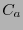 se dice ser aumentado de
se dice ser aumentado de  .
.
Proposición 6.1
Sea
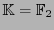 . En todo código lineal ocurre que bien todas sus palabras poseen peso par, o bien el número de las palabras con peso par coincide con el número de las palabras con peso impar.
. En todo código lineal ocurre que bien todas sus palabras poseen peso par, o bien el número de las palabras con peso par coincide con el número de las palabras con peso impar.
En efecto, supóngase que hubiese una palabra de código 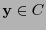 de peso impar. Por un lado, como
de peso impar. Por un lado, como  es un grupo abeliano con la suma, se tiene que la traslación
es un grupo abeliano con la suma, se tiene que la traslación
 es una biyección.
Por otro lado, para cualquier palabra de código
es una biyección.
Por otro lado, para cualquier palabra de código 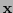 vale que el peso de
vale que el peso de 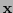 es par si y sólo si el peso de
es par si y sólo si el peso de
 es impar.
Por tanto, la mitad de los elementos de
es impar.
Por tanto, la mitad de los elementos de  posee pesos pares.
posee pesos pares. 
Supondremos en lo sucesivo que
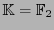 .
.
Sea
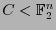 un código lineal. Sea
un código lineal. Sea
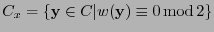 el conjunto de palabras de código con peso par. Entonces
el conjunto de palabras de código con peso par. Entonces 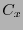 es un código lineal, llamado expurgado de
es un código lineal, llamado expurgado de  . Por la proposición anterior, resulta que bien
. Por la proposición anterior, resulta que bien 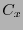 coincide con
coincide con  o bien posee la mitad de elementos de
o bien posee la mitad de elementos de  .
.
Con un tal código se puede decodificar según el siguiente:
- Procedimiento de decodificación.
- Supóngase que al transmitir una palabra
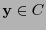 se recibe la palabra
se recibe la palabra
 . Calcúlese la palabra de código
. Calcúlese la palabra de código 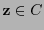 más cercana a
más cercana a 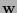 . Si
. Si
 entonces dése a
entonces dése a 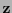 como la palabra
como la palabra 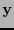 . En otro caso, anúnciese que al menos
. En otro caso, anúnciese que al menos 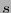 símbolos han cambiado.
símbolos han cambiado.
Supongamos primero que vale la desigualdad (13). Sean 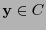 y
y
 tales que
tales que
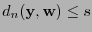 . Para cualquier otra palabra
. Para cualquier otra palabra
 se tiene
se tiene
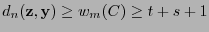 . Por la desigualdad del triángulo se sigue:
. Por la desigualdad del triángulo se sigue:
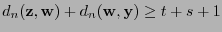 ; y por tanto
; y por tanto
con lo que queda demostrada la relación (12).
Recíprocamente, supongamos que la desigualdad (13) no se cumpliera. Entonces
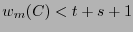 y habría
y habría
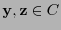 tales que
tales que
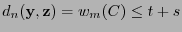 . Elijamos
. Elijamos 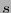 posiciones donde las entradas de
posiciones donde las entradas de 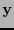 y
y 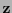 difieran y sea
difieran y sea
 tal que coincida con
tal que coincida con 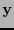 salvo en las
salvo en las 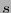 posiciones seleccionadas, donde ha de tomar los valores de
posiciones seleccionadas, donde ha de tomar los valores de 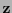 . Entonces
. Entonces
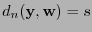 y
y
 . Por tanto,
. Por tanto,
lo cual evidencia que la relación (12) tampoco puede cumplirse. 
De la observación 6.2 se tiene que el extendido del código de Hamming posee un peso mínimo
 , por tanto
, por tanto 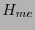 puede corregir un error y detectar dos errores simultáneamente. Se puede pues decodificar como sigue:
puede corregir un error y detectar dos errores simultáneamente. Se puede pues decodificar como sigue:
- Procedimiento de decodificación.
- Supóngase que al transmitir una palabra
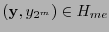 se recibe la palabra
se recibe la palabra
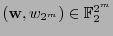 . Calcúlese el síndrome
. Calcúlese el síndrome
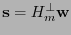 . Si
. Si
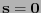 entonces acéptese
entonces acéptese 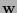 como
como 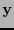 y acaso corríjase
y acaso corríjase 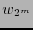 si fuera necesario; en otro caso, si
si fuera necesario; en otro caso, si 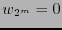 declárese que hubo al menos dos errores y si
declárese que hubo al menos dos errores y si  entonces cámbiese el valor
entonces cámbiese el valor 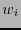 donde
donde  está dado en binario por el síndrome
está dado en binario por el síndrome 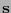 .
.




Siguiente: Códigos de Reed-Muller
Arriba: Introducción a la Teoría
Anterior: Programas
Guillermo M. Luna
2010-05-09
![]() un campo finito y sea
un campo finito y sea
![]() un código lineal-
un código lineal-![]() . Sea
. Sea
![]() definido como sigue:
definido como sigue:
![\begin{displaymath}\forall ({\bf x},x_n)\in\mathbb{K}^n\times\mathbb{K}:\ \left[...
...ightarrow\ {\bf x}\in C\ \&\ x_n = \sum_{j=0}^{n-1} x_j\right].\end{displaymath}](img625.png)
![]() definido como sigue:
definido como sigue:
![]() el espacio generado por
el espacio generado por ![]() y la clase lateral
y la clase lateral ![]() , donde
, donde ![]() es el vector en
es el vector en ![]() constante 1:
constante 1:
![]() .
.
![]() un código lineal. Sea
un código lineal. Sea
![]() el conjunto de palabras de código con peso par. Entonces
el conjunto de palabras de código con peso par. Entonces ![]() es un código lineal, llamado expurgado de
es un código lineal, llamado expurgado de ![]() . Por la proposición anterior, resulta que bien
. Por la proposición anterior, resulta que bien ![]() coincide con
coincide con ![]() o bien posee la mitad de elementos de
o bien posee la mitad de elementos de ![]() .
.
![]() y habría
y habría
![]() tales que
tales que
![]() . Elijamos
. Elijamos ![]() posiciones donde las entradas de
posiciones donde las entradas de ![]() y
y ![]() difieran y sea
difieran y sea
![]() tal que coincida con
tal que coincida con ![]() salvo en las
salvo en las ![]() posiciones seleccionadas, donde ha de tomar los valores de
posiciones seleccionadas, donde ha de tomar los valores de ![]() . Entonces
. Entonces
![]() y
y
![]() . Por tanto,
. Por tanto,
![]() , por tanto
, por tanto ![]() puede corregir un error y detectar dos errores simultáneamente. Se puede pues decodificar como sigue:
puede corregir un error y detectar dos errores simultáneamente. Se puede pues decodificar como sigue: