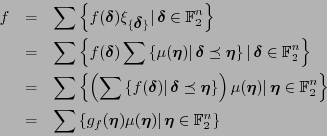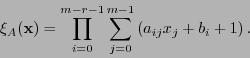Siguiente: Decodificación de códigos de
Arriba: Códigos de Reed-Muller
Anterior: Formas algebraicas
Sea
![$\mathbb{F}_2[X_0,\ldots,X_{n-1}]^{\leq r}$](img742.png) la colección de polinomios con grado a lo sumo
la colección de polinomios con grado a lo sumo 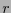 , el cual es un subespacio lineal de
, el cual es un subespacio lineal de
![$\mathbb{F}_2[X_0,\ldots,X_{n-1}]$](img743.png) . Por la observación 7.3, una base de ella es
. Por la observación 7.3, una base de ella es
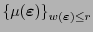 , y es, por tanto, de dimensión
, y es, por tanto, de dimensión
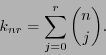 |
(15) |
Definición 7.5 (Reed-Muller)
Para
 , sea
la colección de palabras de código resultantes como evaluaciones de los polinomios de grado a lo sumo
, sea
la colección de palabras de código resultantes como evaluaciones de los polinomios de grado a lo sumo 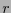 en el espacio
en el espacio
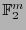 de dimensión
de dimensión 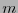 .
.
Se tiene, naturalmente, que  es un código-
es un código-
![$\left[2^m,k_{mr}\right]$](img750.png) , donde
, donde 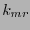 está dado por la ec. (15). Así pues sus palabras de código son de longitud
está dado por la ec. (15). Así pues sus palabras de código son de longitud 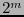 y poseen
y poseen 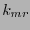 bits de información. Una generatriz de él es la matriz de orden
bits de información. Una generatriz de él es la matriz de orden
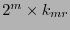 :
:
donde
![$\left\lbrace\mbox{\boldmath$\delta$}_j\right\rbrace_{j\in[\![0,k_{mr}-1]\!]}$](img755.png) es una enumeración de los puntos en
es una enumeración de los puntos en
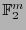 con peso de Hamming a lo sumo
con peso de Hamming a lo sumo 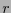 .
.
Por ejemplo, para 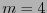 , el código
, el código
 posee como generatriz a
posee como generatriz a
La primera columna contiene los valores, en
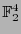 , del único polinomio de grado 0 a saber la constante 1, las siguientes 4 los de las variables
, del único polinomio de grado 0 a saber la constante 1, las siguientes 4 los de las variables 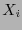 ,
,
![$i\in[\![0,3]\!]$](img760.png) , las siguientes 6 los de las cuadráticas
, las siguientes 6 los de las cuadráticas 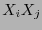 ,
,
![$\{i,j\}\in[\![0,3]\!]^{(2)}$](img762.png) , y las últimas 4 los de las cúbicas
, y las últimas 4 los de las cúbicas 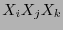 ,
,
![$\{i,j,k\}\in[\![0,3]\!]^{(3)}$](img764.png) . La primera columna contiene
. La primera columna contiene  1's, cada una de las 4 siguientes
1's, cada una de las 4 siguientes 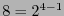 , cada una de las 6 siguientes
, cada una de las 6 siguientes 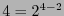 , y cada una de las 4 últimas
, y cada una de las 4 últimas 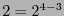 .
.
De la observación 7.4 se sigue:
Proposición 7.1
El dual del código  es el código de Reed-Muller
es el código de Reed-Muller
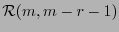 , es decir
, es decir
En efecto, primero se tiene que la dimensión del dual
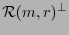 es
es
Así, al ver que
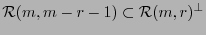 se tendrá que estos espacios coinciden. Para ello si se toma a dos palabras en los códigos
se tendrá que estos espacios coinciden. Para ello si se toma a dos palabras en los códigos
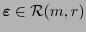 y
y
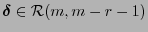 , entonces han de existir dos polinomios
, entonces han de existir dos polinomios
![$f,g\in\mathbb{F}_2[X_0,\ldots,X_{m-1}]$](img777.png) de grados respectivos
de grados respectivos
![$e\in[\![0,r]\!]$](img778.png) ,
,
![$d\in[\![0,m-r-1]\!]$](img779.png) , que producen
, que producen
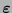 y
y
 al evaluarlos en
al evaluarlos en
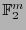 . El producto
. El producto 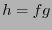 es un polinomio de grado a lo sumo
es un polinomio de grado a lo sumo
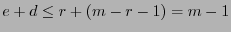 . Por tanto
. Por tanto
![$\left[h(\mbox{\boldmath$\eta$})\right]_{\mbox{\scriptsize\boldmath$\eta$}\in\mathbb{F}_2^m}$](img783.png) es una palabra en el código
es una palabra en el código
 el cual consiste sólo de palabras de peso de Hamming par. Con esto resulta que necesariamente
el cual consiste sólo de palabras de peso de Hamming par. Con esto resulta que necesariamente
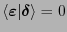 , es decir, esas dos palabras de código son ortogonales.
, es decir, esas dos palabras de código son ortogonales. 
Definición 7.6
Para cualquier conjunto
 su función característica es
su función característica es
 donde
Así,
donde
Así,
 .
.
Se tiene entonces que para cualquier función booleana
 :
:
donde
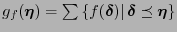 .
.
De manera más precisa:
Observación 7.7
Si
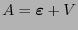 es un conjunto afín, es decir
es un conjunto afín, es decir 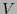 es un espacio lineal en
es un espacio lineal en
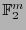 , de dimensión
, de dimensión 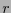 , entonces existe un polinomio
, entonces existe un polinomio
![$f_A\in\mathbb{F}_2[X_0,\ldots,X_{m-1}]$](img798.png) de grado
de grado 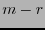 tal que
tal que 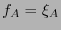 .
.
En efecto, 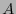 puede ser visto como el conjunto de soluciones de un sistema lineal
puede ser visto como el conjunto de soluciones de un sistema lineal
 de
de 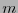 incógnitas y
incógnitas y 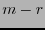 ecuaciones, que puede reescribirse como uno de la forma
ecuaciones, que puede reescribirse como uno de la forma
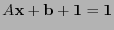 . Entonces
. Entonces
Esta última expresión determina al polinomio 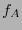 .
. 
De aquí se siguen sin más:
Observación 7.8
El código de Reed-Muller  es el espacio generado por las funciones características de las variedades afines de dimensión al menos
es el espacio generado por las funciones características de las variedades afines de dimensión al menos 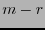 :
:




Siguiente: Decodificación de códigos de
Arriba: Códigos de Reed-Muller
Anterior: Formas algebraicas
Guillermo M. Luna
2010-05-09
![]() la colección de polinomios con grado a lo sumo
la colección de polinomios con grado a lo sumo ![]() , el cual es un subespacio lineal de
, el cual es un subespacio lineal de
![]() . Por la observación 7.3, una base de ella es
. Por la observación 7.3, una base de ella es
![]() , y es, por tanto, de dimensión
, y es, por tanto, de dimensión
![]() , el código
, el código
![]() posee como generatriz a
posee como generatriz a

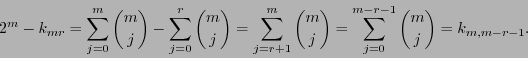
![]() :
: