Siguiente: Códigos cíclicos Arriba: Códigos de Reed-Muller Anterior: Códigos de Reed-Muller

Decodificación de códigos de Reed-Muller

Veremos algunas ideas expuestas en [2] y en su actualización [3].

Se tiene que el código de Reed-Muller ${\cal R}(m,r)$ es un código- $\left[2^m,k_{mr},2^{m-r}\right]$, por tanto, de acuerdo con la observación 4.2, se tiene que puede corregirse con él menos de $\frac{2^{m-r}}{2}=2^{m-r-1}$ errores.

Veamos cómo, habiéndose recibido una palabra $\mbox{\boldmath$\delta$} = \left(\delta_i\right)_{i=0}^{2^m-1}\in\mathbb{F}_2^{2^m}$, cuando se quería transmitir $\mbox{\boldmath$\varepsilon$} = \left(\varepsilon_i\right)_{i=0}^{2^m-1}\in{\cal R}(m,r)$, se corrige hasta $2^{m-r-1}-1$ bits en ella para recuperar la palabra $\mbox{\boldmath$\varepsilon$}\in{\cal R}(m,r)$ en el código más cercana a $\mbox{\boldmath$\delta$}$.

Para $i\in[\![0,2^m-1]\!]$ sea $(i)_2\in\mathbb{F}_2^m$ el vector que coincide con la representación en base-2 de $i$, con $n$ bits, el menos significativo hacia la derecha, y sea $\{(i)_2\}=(i)_2+\{{\bf0}\}$ la mónada que consiste del vector $(i)_2$. Claramente, $\{(i)_2\}$ es una variedad afín de dimensión cero en el hipercubo $\mathbb{F}_2^m$.

Para cada variedad afín $A$ de dimensión $n\in[\![0,r+1]\!]$ en $\mathbb{F}_2^m$, digamos que ésta es par o impar según lo sea $\mbox{card}\{i\in[\![0,2^m-1]\!]\vert\ (i)_2\in A\,\&\,\delta_i\not= \varepsilon_i\}$, es decir, según sea la paridad del número de ``errores'' en $A$.

Pues bien, si $A=\mbox{\boldmath$\varepsilon$}+V$, con $\dim V=r+1$, es una variedad afín de dimensión $r+1$, entonces de acuerdo con la relación (17) si $\mbox{\boldmath$\delta$}$ estuviese en el código, entonces $\langle\xi_A\vert\mbox{\boldmath$\delta$}\rangle =0$. Así pues se tiene que la paridad de $A$ es necesariamente $\langle\xi_A\vert\mbox{\boldmath$\delta$}\rangle$. Consecutivamente, si $A=\mbox{\boldmath$\varepsilon$}+V$, con $\dim V=n\leq r$, es una variedad afín de dimensión $n$, entonces se decidirá si es par o impar por mayoría de votos: Se ha de tener que $A$ está incluída en un número impar de variedades afines de dimensión $n+1$, algunas pares y otras impares. La paridad de $A$ será aquella que resulte mayoritaria entre estas últimas.

Proposición 7.2   Si $A$ es una variedad afín de dimensión $n$ en $\mathbb{F}_2^m$, entonces está incluída en exactamente $2^{m-n}-1$ variedades afines de dimensión $n+1$. De hecho cada uno de los puntos en el complemento de $A$ pertenece a una única de tales variedades afines.

En efecto, supongamos $A=\mbox{\boldmath$\varepsilon$}+V$, con $\dim V=n$. Veremos primero que el subsepacio $V$ está en $2^{m-n}-1$ subespacios de dimensión $n+1$. Si $\mbox{\boldmath$\varepsilon$}_1\not\in V$ entonces $V\oplus \mbox{\boldmath$\varepsilon$}_1=\{{\bf v}+t \mbox{\boldmath$\varepsilon$}_1\vert\ {\bf v}\in V\,,\,t\in\mathbb{F}_2\}$ es un subespacio de dimensión $n+1$ que contiene a $V$. Ahora bien, se tiene $V\oplus \mbox{\boldmath$\varepsilon$}_1= V\oplus \mbox{\boldmath$\varepsilon$}_2$ si y sólo si $\mbox{\boldmath$\varepsilon$}_1- \mbox{\boldmath$\varepsilon$}_2\in V$. Así pues, el número de espacios distintos de la forma $V\oplus \mbox{\boldmath$\varepsilon$}$ coincide con el de clases laterales que define $V$.

Ya que la cardinalidad del espacio cociente $\mathbb{F}_2^m/V$ es $\frac{2^m}{2^n}=2^{m-n}$, se tiene que el número de subespacios de dimensión $n+1$ que contienen a $V$ es $2^{m-n}-1$ (ésos son de la forma $V\oplus \mbox{\boldmath$\varepsilon$}$ con $\mbox{\boldmath$\varepsilon$}\not={\bf0}$).

Ahora bien, $A'=\mbox{\boldmath$\varepsilon$}+V'$ es una extensión de dimensión $n+1$ de $A=\mbox{\boldmath$\varepsilon$}+V$ si y sólo si $V'$ es una extensión de dimensión $n+1$ de $V$. Por tanto hay $2^{m-n}-1$ de tales extensiones. $\Box$

Proposición 7.3   Si $\mbox{\boldmath$\delta$} = \left(\delta_i\right)_{i=0}^{2^m-1}\in\mathbb{F}_2^{2^m}$ involucra menos de $2^{m-r-1}$ errores, entonces siempre que $A$ sea una variedad afín de dimensión $n\leq r$ en $\mathbb{F}_2^m$, su paridad coincidirá con la paridad mayoritaria entre las variedades de dimensión $n+1$ que contengan a $A$.

En efecto, supongamos que se haya cometido $t < 2^{m-r-1}$ errores. Sea $A$ una variedad afín de dimensión $r$ en $\mathbb{F}_2^m$ y sean $(i_1)_2,\ldots(i_s)_2$ los errores cometidos fuera de $A$. Por un lado $2t<2^{m-r}-1$ y en consecuencia $t<(2^{m-r}-1)-t$. El lado izquierdo es una cota superior de $s$, que cuenta el número de errores fuera de $A$. El lado derecho, en cambio, cuenta el número de espacios de dimensión $r$ en donde no hay error. Por tanto todos estos espacios han de tener la misma paridad que $A$, y ellos son más.

Este argumento se lleva a dimensiones menores. $\Box$

Procedimiento de decodificación

Habiendo recibido $\mbox{\boldmath$\delta$} = \left(\delta_i\right)_{i=0}^{2^m-1}\in\mathbb{F}_2^{2^m}$:

Paso inicial.

Para cada variedad afín $A$ de dimensión $r+1$ declárese par o impar según sea el valor $\langle\xi_A\vert\mbox{\boldmath$\delta$}\rangle$.

Paso recursivo.

Para cada $n=r,\ldots,1,0$ declárese a cada variedad afín $A$ de dimensión $n$ según haya sido declarada la mayoría de las variedades de dimensión $n+1$ que contengan a $A$.

Paso final.

En las variedades de dimensión 0, aquellas que sean impares dan los índices en donde hay que cambiar el valor de $\mbox{\boldmath$\delta$}$.

El número de conjuntos linealmente independientes de cardinalidad $k$ en $\mathbb{F}_2^n$ es $\alpha_{nk} = \prod_{\kappa=0}^{k-1}(2^n-2^{\kappa})$. Evidentemente, el número de bases de un espacio de dimensión $k$ es $\alpha_{kk}$. Así, el número de espacios de dimensión $k$ en $\mathbb{F}_2^n$ es

$$\beta_{nk} = \frac{\alpha_{nk}}{\alpha_{kk}} = \prod_{\kappa=... ...1} = \prod_{\kappa=1}^{k}\frac{2^{n-k+\kappa}-1}{2^{\kappa}-1}.$$

Ya que cada espacio de dimensión $k$ determina $2^{n-k}$ variedades afines paralelas a él, se tiene finalmente que el número de variedades afines de dimensión $k$ en $\mathbb{F}_2^n$ es

$$2^{n-k}\beta_{nk} = 2^n \prod_{\kappa=1}^{k}\frac{2^{n-k+\kappa}-1}{2(2^{\kappa}-1)}.$$ (18)

De hecho este método de recuento de variedades afines sirve de base para diseñar uno que permita enumerar, una a una, las variedades afines de dimensión $r+1$ requeridas en el ``Paso inicial'' del algoritmo de decodificación de Reed-Muller.

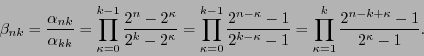
El ``Paso recursivo'' se puede realizar enumerando a las variedades de dimensión mayor en uno que la actual y que la contienen utilizando la proposición 7.2.

Siguiente: Códigos cíclicos Arriba: Códigos de Reed-Muller Anterior: Códigos de Reed-Muller