Siguiente: Método PGZ Arriba: Códigos cíclicos Anterior: Códigos RS: Como códigos

Decodificación de Reed-Solomon

Sea $q$ una potencia de un número primo y sea $k\leq q-1$. Supongamos que para una palabra $\sigma\in\mathbb{F}_q^k$, su código correspondiente a $\mbox{\rm RS}(q-1,k)$ es $f(X) = \sum_{\lambda=0}^{q-2} f_{\lambda} X^{\lambda}\in\mathbb{F}_q[X]$, pero que, al ser transmitido, el destinatario hubiera recibido $h(X) = \sum_{\lambda=0}^{q-2} h_{\lambda} X^{\lambda}$. El propósito de la decodificación es recuperar $f(X)$ a partir de $h(X)$ o, en otras palabras, calcular el error $e(X)=h(X)-f(X)$. Naturalmente, la recuperación de $\sigma$ a partir de $f(X)$ se hace dividiendo a este último entre el polinomio $g_{q-1,k}(X)$.

Para cada $\kappa\in[\![1,q-1-k]\!]$ denotemos por $s_{\kappa}$ al síndrome $s_{\kappa} = e(a^{\kappa}) = h(a^{\kappa})$ (pues $f(a^{\kappa})=0$).

Inicialmente, consideremos el caso $k=1$.

Supongamos que el error entre $h(X)$ y $f(X)$ ocurre solamente en un ``byte'', es decir, en un solo coeficiente, digamos $h_{\lambda}$. Entonces los síndromes han de satisfacer $s_1=e_{\lambda}a^{\lambda}$ y $s_2=e_{\lambda}a^{2\lambda}$. Por tanto $a^{\lambda} = \frac{s_2}{s_1}$ y, en consecuencia, $e_{\lambda} = \frac{s_1^2}{s_2}$. Así pues:

Decodificación de Reed-Solomon para $k=1$. Si sólo hay un error en un solo coeficiente, la posición en la que ocurre es $\lambda = \log_a\left(\frac{s_2}{s_1}\right)$ y el coeficiente del error ahí es $e_{\lambda} = \frac{s_1^2}{s_2}$.

Para $k>1$, sea $E\subset[\![0,q-2]\!]$ el conjunto de índices $\lambda$ tales que $e_{\lambda} \not= 0$. Entonces se tiene el sistema de ecuaciones lineales:

$$\forall\kappa\in[\![0,q-1-k]\!]:\ \ s_{\kappa} = \sum_{\lambda\in E} e_{\lambda}a^{\kappa\lambda}$$ (27)

con soluciones únicas siempre que $2\,\mbox{\rm card}\,(E)\leq q-1-k$. Sin embargo éste no determina al conjunto de índices $E$.

Para determinarlo es necesaria una labor suplementaria. Se define el polinomio localizador de errores como

$$\rho(X) = \prod_{\lambda\in E} (X-a^{-\lambda}).$$ (28)

el cual es un polinomio mónico. Entonces las raíces de $\rho(X)$ son precisamente las potencias $a^{-\lambda}$ con $\lambda\in E$. También se define el polinomio evaluador de errores como

$$\omega(X) = \sum_{\lambda\in E} e_{\lambda} \prod_{\ell\in E-\{\lambda\}} (X-a^{-\ell}).$$ (29)

Se tiene $\mbox{\rm grd}\,(\rho(X)) = \mbox{\rm card}\,(E)$ y $\mbox{\rm grd}\,(\omega(X)) = \mbox{\rm card}\,(E)-1$. Se supondrá $2\,\mbox{\rm card}\,(E)\leq q-1-k$.

Proposición 8.4   Los polinomios $\rho(X)$ y $\omega(X)$ son primos relativos y

$$\forall\lambda\in E:\ e_{\lambda} = \frac{\omega(a^{-\lambda})}{\rho'(a^{-\lambda})},$$ (30)

donde $\rho'(X)$ es la derivada formal del polinomio $\rho(X)$.

En efecto, para lo primero observamos que $\rho(X)$ y $\omega(X)$ no pueden tener raíces comunes:

$$\begin{eqnarray*} \rho(x) = 0 &\Longrightarrow& x = a^{-\lambda}\ \mbox{ para al... ... a^{-\ell}) \\ &\Longrightarrow& \omega(a^{-\lambda}) \not= 0. \end{eqnarray*}$$

Para lo segundo, por la fórmula de Leibniz, la derivada formal de $\rho(X)$ es

$$\rho'(X) = \sum_{\lambda\in E} \prod_{\ell\in E-\{\lambda\}} (X-a^{-\ell})$$

y por tanto $\rho'(a^{-\lambda}) = \prod_{\ell\in E-\{\lambda\}} (a^{-\lambda} - a^{-\ell})$. Así resulta la expresión (30). $\Box$

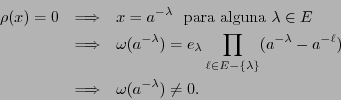
Si se determinara el polinomio localizador de errores $\rho(X)$ entonces sus raíces determinan a su vez el conjunto $E$. Consideremos un tercer polinomio, llamado de síndromes, pues éstos son sus coeficientes:

$$\sigma(X) = s_1 + s_2X + \cdots + s_{q-1-k}X^{q-2-k} = \sum_{\kappa=0}^{q-2-k}s_{\kappa+1}X^{\kappa}.$$

Proposición 8.5   Existe un polinomio $\mu(X)\in\mathbb{F}_q[X]$ tal que se cumple la ecuación clave:

$$\rho(X) \sigma(X) = \mu(X)\,X^{q-1-k} - \omega(X).$$ (31)

O equivalentemente:

$$\rho(X) \sigma(X) = - \omega(X) \bmod X^{q-1-k}.$$

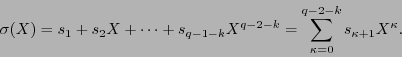
En efecto, un cálculo directo da:

$$\sigma(X) = \sum_{\kappa=0}^{q-2-k}\,e(a^{\kappa+1})\,X^{\kappa}$$

$$= \sum_{\kappa=0}^{q-2-k}\left[\sum_{\lambda\in E}e_{\lambda}a^{(\kappa+1)\lambda}\right]X^{\kappa}$$

$$= \sum_{\lambda\in E}e_{\lambda}a^{\lambda}\left[\sum_{\kappa=0}^{q-2-k}\left(a^{\lambda}X\right)^{\kappa}\right]$$

$$= \sum_{\lambda\in E}e_{\lambda}\left[\frac{\left(a^{\lambda}X\right)^{q-1-k}-1}{X-a^{-\lambda}}\right] ,%\\$$ (32)

de donde

$$\begin{eqnarray*} \rho(X) \sigma(X) &=& \sum_{\lambda\in E} e_{\lambda}\left[\le... ...l}) \right] - \omega(X) \\ &=& X^{q-1-k}\,\mu(X) - \omega(X) . \end{eqnarray*}$$

$\Box$

Así pues, para decodificar, habiendo calculado el polinomio de síndromes $\sigma(X)$, se ha de determinar a los polinomios localizador y evaluador de errores $\rho(X)$ y $\omega(X)$ de manera que se cumpla la ecuación clave (31).

Siguiente: Método PGZ Arriba: Códigos cíclicos Anterior: Códigos RS: Como códigos