



Siguiente: Método de Euclides
Arriba: Decodificación de Reed-Solomon
Anterior: Decodificación de Reed-Solomon
Método PGZ
Veamos una primera forma de resolver la ecuación clave, mediante el llamado decodificador de Peterson-Gorenstein-Zierler (PGZ).
Supongamos que hubieran ocurrido 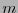 errores, con
errores, con  . Escribamos a los polinomios localizador y evaluador de errores como:
. Escribamos a los polinomios localizador y evaluador de errores como:
El producto
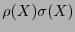 es de grado a lo sumo
es de grado a lo sumo 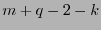 , pero para
, pero para
![$j\in[\![m,q-2-k]\!]$](img1155.png) la ecuación clave implica que el coeficiente correspondiente en ese producto es nulo. Por la manera en la que se multiplica a los polinomios, se ha de tener pues:
la ecuación clave implica que el coeficiente correspondiente en ese producto es nulo. Por la manera en la que se multiplica a los polinomios, se ha de tener pues:
Puesto que 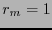 , se tiene:
, se tiene:
Estas condiciones plantean, de forma matricial, el sistema de ecuaciones:
![\begin{displaymath}
\left[\begin{array}{lllcl}
s_{m+1} & s_{m} & s_{m-1} & \cdot...
...1 \\ s_2 \\ s_3 \\ \vdots \\ s_{q-k-(1+m)}
\end{array}\right]
\end{displaymath}](img1159.png) |
(33) |
o sea
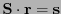 , donde
, donde
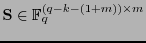 ,
,
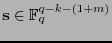 y
y
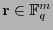 es el vector de coeficientes de
es el vector de coeficientes de 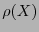 y hace aquí el papel de incógnita. El sistema (33) está sobredimensionado (hay más condiciones que incógnitas), puede pues resolverse tomando solamente sus primeros
y hace aquí el papel de incógnita. El sistema (33) está sobredimensionado (hay más condiciones que incógnitas), puede pues resolverse tomando solamente sus primeros 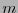 renglones. Queda el sistema:
renglones. Queda el sistema:
Como los síndromes son no nulos, y 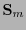 es una matriz definida por diagonales, se tiene que es no-singular. Por tanto el polinomio localizador de errores se obtiene como
es una matriz definida por diagonales, se tiene que es no-singular. Por tanto el polinomio localizador de errores se obtiene como
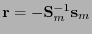 .
.
Habiendo así localizado el conjunto 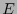 , el sistema (27) permite entonces calcular el error
, el sistema (27) permite entonces calcular el error 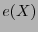 , con lo cual se ha de completar el proceso de decodificación.
, con lo cual se ha de completar el proceso de decodificación.
También puede verse que si
![$m'\in[\![m+1,q-1-k]\!]$](img1170.png) entonces
entonces 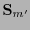 es singular. Así pues, si se desconociera cuál es el valor de
es singular. Así pues, si se desconociera cuál es el valor de 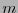 , entonces éste se obtendría como el máximo
, entonces éste se obtendría como el máximo 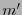 tal que
tal que 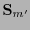 es no-singular.
es no-singular.




Siguiente: Método de Euclides
Arriba: Decodificación de Reed-Solomon
Anterior: Decodificación de Reed-Solomon
Guillermo M. Luna
2010-05-09
![]() errores, con
errores, con ![]() . Escribamos a los polinomios localizador y evaluador de errores como:
. Escribamos a los polinomios localizador y evaluador de errores como:
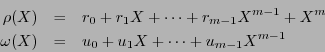
![\begin{displaymath}j\in[\![m,q-2-k]\!]\ \Rightarrow\ \sum_{\ell=0}^mr_{\ell}s_{j+1-\ell} = 0.\end{displaymath}](img1156.png)
![\begin{displaymath}j\in[\![m,q-2-k]\!]\ \Rightarrow\ \sum_{\ell=0}^{m-1}r_{\ell}s_{j+1-\ell} = -s_{j+1-m}.\end{displaymath}](img1158.png)
![]() , el sistema (27) permite entonces calcular el error
, el sistema (27) permite entonces calcular el error ![]() , con lo cual se ha de completar el proceso de decodificación.
, con lo cual se ha de completar el proceso de decodificación.
![]() entonces
entonces ![]() es singular. Así pues, si se desconociera cuál es el valor de
es singular. Así pues, si se desconociera cuál es el valor de ![]() , entonces éste se obtendría como el máximo
, entonces éste se obtendría como el máximo ![]() tal que
tal que ![]() es no-singular.
es no-singular.