Siguiente: Códigos BCH Arriba: Decodificación de Reed-Solomon Anterior: Método PGZ

Método de Euclides

Escribiendo la ecuación clave como

$$\mu(X)\,X^{q-1-k}+(-\rho(X)) \sigma(X) = - \omega(X)$$

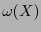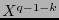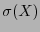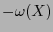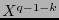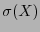tenemos que $\omega(X)$ es un máximo común divisor (salvo por el signo) de $X^{q-1-k}$ y el polinomio de síndromes $\sigma(X)$. Así pues, utilizando el Algoritmo de Euclides, al calcular una forma extendida del Máximo Común Divisor y expresar a $- \omega(X)$ como una combinación lineal de $X^{q-1-k}$ y $\sigma(X)$ se obtendrá los polinomios 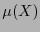$\mu(X)$ y el localizador de errores 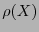$\rho(X)$. Este último determina el conjunto 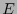$E$ y el sistema (27) permite entonces calcular el error 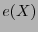$e(X)$, con lo cual se ha de completar el proceso de decodificación.