Siguiente: Una segunda presentación Arriba: Códigos BCH Anterior: Códigos BCH

Una primera presentación

Como en la sección anterior, aquí seguiremos la presentación hecha en [4].

Sea $q_1$ una potencia de un primo $p$, sea $k\leq q_1-1$ y $q_0$ tal que $\mathbb{F}_{q_0}$ sea un subcampo de $\mathbb{F}_{q_1}$. El correspondiente código BCH es el $\mathbb{F}_{q_0}$-subespacio lineal $C$ de $\mbox{\rm RS}(q_1-1,k)$ tal que $C\subset\mathbb{F}_{q_0}[X]$.

Sea $g_{q_1-1,k}(X) = \prod_{i=1}^{q_1-1-k} (X-a^i)$ el polinomio generador de $\mbox{\rm RS}(q_1-1,k)$, donde $a$ es un elemento primitivo de $\mathbb{F}_{q_1}$. Entonces $g_{q_1-1,k}(a^i)=0$ siempre que $i\in[\![1,q_1-1-k]\!]$. Por tanto, si un polinomio $\pi(X)\in\mathbb{F}_{q_1}[X]$ está en el código BCH $C$ entonces $\pi(X)\in\mathbb{F}_{q_0}[X]$ y $\pi(a^i)=0$ para todo $i\in[\![1,q_1-1-k]\!]$.

De su definición, no se desprende inmediatamente cuáles serán la longitud, la dimensión y la distancia mínima de un código BCH $C$. Sin embargo, la distancia mínima $q_1-1-k$ de $\mbox{\rm RS}(q_1-1,k)$ se dice ser la distancia prevista del código $C$.

Observación 8.7   Sean $q=p^n$, $x\in\mathbb{F}_{q}$ y $p_x(X)\in\mathbb{F}_{p}[X]$ el polinomio mínimo respecto a $\mathbb{F}_{p}$.

• Como $x^{q}=1$ se tiene $p_x(X)\vert(X^{q}-1)$ en $\mathbb{F}_{p}[X]$.
• Por otro lado, sea $n_x=\mbox{\rm grd}\,p_x(X)$ el grado del polinomio mínimo. Se tiene que el conjunto $L=\{1,x,\ldots,x^{n_x-1}\}$ es linealmente independiente, respecto a $\mathbb{F}_{p}$, pero $L\cup\{x^{n_x}\}$ no lo es. Por tanto $n_x\leq n$.
• En particular, si $x$ es primitivo, entonces $n_x=n$.

Observación 8.8   Sean $n_0,n_1\in\mathbb{N}$ tales que $n_0\vert n_1$, $p$ un número primo, $q_0=p^{n_0}$ y $q_1=p^{n_1}$. Sea $a_1\in\mathbb{F}_{q_1}$ un elemento primitivo en ese campo. Sea $m=\frac{q_1-1}{q_0-1}$ y $a_0=a_1^m$. Entonces $a_0$ es generador de un subgrupo $\langle a_0\rangle$, isomorfo a $\mathbb{F}_{q_0}^*$, de $\mathbb{F}_{q_1}^*$. De hecho, $\langle a_0\rangle\cup\{0\}$ es un subcampo de $\mathbb{F}_{q_1}$, isomorfo a $\mathbb{F}_{q_0}$.

En estas condiciones, si $p_{a_0}(X)$ es el polinomio mínimo de $a_0$ respecto a $\langle a_0\rangle\cup\{0\}$, entonces $\mathbb{F}_{q_1}/(p_{a_0}(X))$ es isomorfo a $\mathbb{F}_{q_0}$. En consecuencia, $\mbox{\rm grd}\,p_{a_0}(X) = n_0$.

Supongamos ahora que $\mathbb{F}_{q_0}$ es un subcampo de $\mathbb{F}_{q_1}$. Veamos cómo calcular polinomios mínimos de elementos en $\mathbb{F}_{q_1}$ respecto a $\mathbb{F}_{q_0}$.

Se dice que dos elementos $y,z\in\mathbb{F}_{q_1}$ son conjugados respecto a $\mathbb{F}_{q_0}$, si existen $x\in\mathbb{F}_{q_1}$ e $i,j\in[\![0,\frac{n_1}{n_0}-1]\!]$ tales que $y=x^{q_0^i}$ y $z=x^{q_0^j}$. Esto introduce una relación de equivalencia en $\mathbb{F}_{q_1}$.

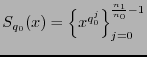Para cada $x\in\mathbb{F}_{q_1}$, sea $S_{q_0}(x) =\left\{x^{q_0^j}\right\}_{j=0}^{\frac{n_1}{n_0}-1}$ (naturalmente para $j=\frac{n_1}{n_0}$, $q_0^j = (p^{n_0})^j = p^{n_1} = q_1,$ por tanto $x^{q_0^j} = x^{q_1} = x$). Así cada $S_{q_0}(x)$ es una clase de conjugación y posee $\frac{n_1}{n_0}$ elementos.

Debido a que la transformación $z\mapsto z^{q_0}$ es un homomorfismo $\mathbb{F}_{q_1}\to\mathbb{F}_{q_1}$ se tiene:

Observación 8.9   Si $\pi(X)\in\mathbb{F}_{q_0}[X]$ entonces rige la implicación siguiente:

$$\forall x\in\mathbb{F}_{q_1}:\ \left[\pi(x)=0\ \ \Longrightarrow\ \ \pi(x^{q_0})=0\right].$$

Por tanto, los conjugados de raíces de polinomios con coeficientes en el subcampo son también raíces de esos polinomios. Así, si $a$ es primitivo en $\mathbb{F}_{q_1}$ y $\pi(X)$ está en el código BCH entonces las potencias $a^i$, con $i\in[\![1,q_1-1-k]\!]$, y sus conjugados son raíces de $\pi(X)$.

Proposición 8.6   Para cada $x\in\mathbb{F}_{q_1}$, el polinomio mínimo $p_{x}(X)$ respecto a $\mathbb{F}_{q_0}$ queda caracterizado como

$$p_{x}(X) = \prod_{y\in S_{q_0}(x)}\left(X-y\right).$$ (35)

Se demuestra la proposición viendo que al expandir la expresión a la derecha de (35) resulta un polinomio con coeficientes en $\mathbb{F}_{q_0}$, irreducible ahí y que es el de grado mínimo que se anula en $x$. $\Box$

Sean $a$ un elemento primitivo en $\mathbb{F}_{q_1}$ y $g_{q_1-1,k}(X) = \prod_{i=1}^{q_1-1-k} (X-a^i)$ el generador de $\mbox{\rm RS}(q_1-1,k)$. Si $\pi(X)$ está en el correspondiente código BCH, entonces $\pi(a^i)=0$, con $i\in[\![1,q_1-1-k]\!]$. Por tanto, cada uno de los polinomios mínimos $p_{a^i}(X)$, respecto al subcampo $\mathbb{F}_{q_0}$, divide a $\pi(X)$. En consecuencia, el mínimo común múltiplo $\mbox{\rm mcm}\left\{p_{a^i}(X)\right\}_{j=1}^{q_1-1-k}$ también divide a $\pi(X)$. En particular, debe dividir también al generador $g_{q_1-1,k}(X)$. Por la minimalidad de este último, necesariamente se ha de tener: $g_{q_1-1,k}(X) = \mbox{\rm mcm}\left\{p_{a^i}(X)\right\}_{j=1}^{q_1-1-k}.$

Siguiente: Una segunda presentación Arriba: Códigos BCH Anterior: Códigos BCH