



Next: Variedades tóricas
Up: Variedades tóricas
Previous: Conos
Contents
Index
Abanicos
Sea
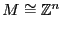 un retículo y sea
un retículo y sea
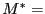 Hom
Hom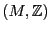 su retículo dual. Se tiene pues una transformación bilineal
su retículo dual. Se tiene pues una transformación bilineal
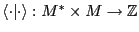 . Extendiendo los retículos a
. Extendiendo los retículos a
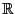 , se tiene una transformación bilineal
, se tiene una transformación bilineal
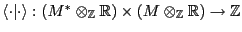 .
.
Un cono poliédrico racional fuertemente convexo es un conjunto
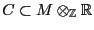 tal que
tal que
- es un cono:
![$ \left[{\bf x}\in C , r\in\mathbb{R}^+ \Longrightarrow r{\bf x}\in C\right]$](img585.png) ,
,
- es un poliedro, es decir, la intersección de un número finito de semiespacios,
- es racional, es decir, los semiespacios que lo determinan a su vez están determinados por ecuaciones polinomiales con coeficientes en
 ,
,
- y es fuertemente convexo, es decir, el único espacio lineal que contiene es la mónada que consta del origen.
El dual del cono 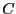 es
es
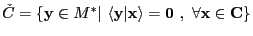 . Una cara de
. Una cara de 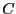 es de la forma
es de la forma
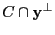 para alguna
para alguna
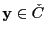 .
.
Un abanico (fan) en 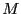 es una colección finita
es una colección finita 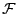 de poliedros racionales fuertemente convexos tal que
de poliedros racionales fuertemente convexos tal que
- toda cara de un cono en
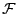 es un cono en
es un cono en 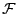 , y
, y
- la intersección de cualesquiera dos conos en
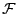 es una cara de cada uno de esos conos.
es una cara de cada uno de esos conos.
El soporte del abanico es
Spt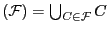 . Un abanico puede verse como una descomposición de
. Un abanico puede verse como una descomposición de
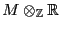 por poliedros racionales fuertemente convexos.
por poliedros racionales fuertemente convexos.
Para un cono
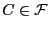 sea
sea
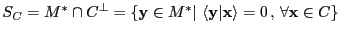 .
.




Next: Variedades tóricas
Up: Variedades tóricas
Previous: Conos
Contents
Index
Guillermo Morales-Luna
2011-10-19
![]() un retículo y sea
un retículo y sea
![]() Hom
Hom![]() su retículo dual. Se tiene pues una transformación bilineal
su retículo dual. Se tiene pues una transformación bilineal
![]() . Extendiendo los retículos a
. Extendiendo los retículos a
![]() , se tiene una transformación bilineal
, se tiene una transformación bilineal
![]() .
.
![]() tal que
tal que
![]() es una colección finita
es una colección finita ![]() de poliedros racionales fuertemente convexos tal que
de poliedros racionales fuertemente convexos tal que
![]() sea
sea
![]() .
.
![]() que cumple con las propiedades anteriores es de la forma
que cumple con las propiedades anteriores es de la forma ![]() para algún cono
para algún cono
![]() poliédrico racional fuertemente convexo.
poliédrico racional fuertemente convexo.