Variedades tóricas

Un grupo algebraico es una variedad proyectiva tal que su producto $\cdot:G\times G\to G$ y su inversa $\cdot^{-1}:G\to G$ son sendos morfismos.

Por ejemplo, si $\mathbb{K}$ es un campo y $n\geq 1$ , el grupo $G=$GL$_n(\mathbb{K})$ es algebraico, pues es una variedad en $\mathbb{K}^{n\times n}$ , la imagen inversa de $\mathbb{K}-\{0\}$ bajo la función de determinante, y además las operaciones son morfismos.

Un grupo lineal algebraico es un grupo algebraico $G$ que es en sí una variedad afín.

Una variedad abeliana es un grupo algebraico que es una variedad proyectiva y conexa.

El producto de grupos algebraicos es un grupo algebraico.

Las operaciones de un grupo algebraico definen homomorfismos en el anillo de coordenadas $\mathbb{K}[G]\to\mathbb{K}[G]\otimes\mathbb{K}[G]$ y $\mathbb{K}[G]\to\mathbb{K}[G]$ .

Sean $G_{\cdot}=$GL$_1(\mathbb{K})$ y $G_+<$GL$_2(\mathbb{K})$ el subgrupo correspondiente a las matrices triangulares superiores con 1 en la diagonal. Se tiene que $G_{\cdot}$ es el grupo multiplicativo de $\mathbb{K}$ y $G_+$ su grupo aditivo. Para cada $k\geq 1$ , el grupo algebraico $G_{\cdot}^k$ es un toro.

Sean $A$ una variedad, $G$ un grupo algebraico y $\pi:G\times A\to A$ una acción de grupo. Se dice que $\pi$ es algebraica si es un morfismo.

Una variedad proyectiva $A$ es una variedad tórica si es irreducible, normal y posee un subconjunto $U$ abierto, denso, isomorfo a un toro tal que la acción natural de $U$ sobre sí mismo se extiende a $A$ .

Sean $G$ y $H$ dos grupos algebraicos y $A$ , $B$ sendas variedades sobre las que actúan $G$ y $H$ respectivamente. Sea $\rho:G\to H$ un homomorfismo de grupos. Un morfismo $\phi:A\to B$ se dice $\rho$ -equivariante si conmuta con las acciones de $G$ y $H$ , es decir: $\forall (g,a)\in G\times A: \pi_B(\rho(g),\phi(a)) = \phi(\pi_A(g,a)),$

$$\xymatrix{ G\times A \ar[r]^{\pi_A} \ar[d]_{(\rho,\phi)} & A \ar[d]^{\phi} \ H\times B \ar[r]_{\pi_B} & B <tex2html_comment_mark>11 }$$ (13)

Si $A$ , $B$ son variedades tóricas y $G$ y $H$ son los toros densos insertos entonces $\phi$ se dice ser un morfismo tórico.

Proposición 3.5   Toda variedad tórica se puede poner en correspondencia biunívoca con un abanico, acaso bajo la acción de un elemento en SL$(n,\mathbb{Z})$ .

Sea $M=\mathbb{Z}^m$ el retículo de coordenadas enteras, el cual es un $\mathbb{Z}$ -módulo, también de dimensión $m$ . Se tiene que Hom$(M,\mathbb{Z}) = M^* \cong M$ . Sea $\mathbb{T}_m=(\mathbb{C}^*)^m$ el toro algebraico de dimensión $m$ , el cual es un grupo multiplicativo, y sea $\mathbb{T}_m^* =$   Hom$(M^*,\mathbb{C}^*) = M\otimes_{\mathbb{Z}}\mathbb{C}^*$ .

Cada ${\bf x}\in M$ determina un carácter $\varepsilon({\bf x}):\mathbb{T}_m\to\mathbb{C}^*$ , ${\bf z}\mapsto\varepsilon({\bf x})({\bf z}) = \prod_{\mu=0}^{m-1}z_{\mu}^{x_{\mu}}$ . Naturalmente, se tiene $\varepsilon({\bf0}) = 1$ y $\varepsilon({\bf x}_0+{\bf x}_1) = \varepsilon({\bf x}_0)\cdot \varepsilon({\bf x}_1)$ . Así pues, $\varepsilon$ es un homomorfismo de $M$ al grupo de caracteres de $\mathbb{T}_m$ .

También se tiene que cada punto ${\bf x}\in M$ determina una transformación $\gamma_{{\bf x}}:\mathbb{C}^*\to\mathbb{T}_m^*$ , $z\mapsto\gamma_{{\bf x}}(z)$ , donde $\forall {\bf y}\in M^*$ , $\langle \gamma_{{\bf x}}(z)\vert{\bf y} \rangle = z^{\langle {\bf y}\vert{\bf x} \rangle }$ . Aquí también $\gamma_{\bf0} = 1$ y $\gamma_{{\bf y}_0+{\bf y}_1} = \gamma_{{\bf y}_0}\cdot\gamma_{{\bf y}_1}$ . La imagen de $\gamma:{\bf x}\mapsto\gamma_{{\bf x}}$ se dice ser un grupo uniparametrizado (one-parameter group), entonces $\gamma$ es en sí un homomorfismo de grupos.

Sea ${\bf x}_0,\ldots,{\bf x}_{m-1}$ una base de $M$ y sea ${\bf y}_0,\ldots,{\bf y}_{m-1}$ la correspondiente base dual del dual $M^*$ . Entonces la transformación $T_m^*\to T_m$ , $\phi\mapsto\left(\langle \phi\vert{\bf x}_i \rangle \right)_{i=0}^{m-1}$ es un isomorfismo de grupos.

Para cada $i\in[\![0,m-1]\!]$ sea $\phi_i=\varepsilon({\bf x}_i)$ . Entonces $\left(\phi_i\right)_{i=0}^{m-1}$ es un sistema de coordenadas para $T_m^*$ .

Sea $S_C=\langle{\bf y}_0,\ldots,{\bf y}_{p-1}\rangle_{\mathbb{Z}^+}$ un semigrupo finitamente generado, determinado por un cono poliédrico fuertemente convexo $C\subset M\otimes_{\mathbb{Z}}\mathbb{R}$ . Sea

$$U_C = \{{\bf u}:S_C\to\mathbb{C}\vert {\bf u}({\bf0}) = 1 \& {... ...u}({\bf z}_0)\cdot {\bf u}({\bf z}_1) , \forall {\bf z}_0,{\bf z}_1\in S_C\}.$$

Entonces $U_C$ se identifica naturalmente con un subconjunto de $\mathbb{C}^p$ .

Proposición 3.6   Sea $C\subset M\otimes_{\mathbb{Z}}\mathbb{R}$ un cono poliédrico fuertemente convexo, entonces su dual $\check{C}$ es un cono poliédrico fuertemente convexo en $M^*\otimes_{\mathbb{Z}}\mathbb{R}$ .

Si $D\subset C$ es una cara entonces existe un funcional ${\bf z}\in M^*\cap\check{C}$ tal que $D=C\cap{\bf z}^{\perp}$ por lo cual $D$ es también un cono poliédrico fuertemente convexo. Se tendrá $S_D = S_C+\langle-{\bf z}\rangle_{\mathbb{Z}^+}$ , $U_D = \{{\bf u}\in U_C\vert \langle {\bf z}\vert{\bf u} \rangle \not=0\}$ y éste es un conjunto abierto en $U_C$ .

Teorema 3.1   Sea ${\cal F}$ un abanico en $M$ . Entonces se puede pegar de manera natural a los conjuntos en $\left(U_C\right)_{C\in{\cal F}}$ para obtener un espacio de Haussdorff

Emb$$({\cal F}) = \bigcup_{C\in{\cal F}}U_C,$$

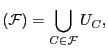
el cual es una variedad tórica de dimensión $m$ , llamada inmersión toral asociada al abanico $(M,{\cal F})$ .