Sea
![]() una colección de
una colección de ![]() variables formales. El anillo de polinomios de Laurent es
variables formales. El anillo de polinomios de Laurent es
![]() . Sea
. Sea
![]() el homomorfismo
el homomorfismo
![]() que identifica al retículo
que identifica al retículo
![]() , y su estructura aditiva, con los monomios de Laurent, y su estructura multiplicativa.
, y su estructura aditiva, con los monomios de Laurent, y su estructura multiplicativa.
Para un polinomio de Laurent
![]() , donde
, donde
![]() es un conjunto finito, se define el soporte de
es un conjunto finito, se define el soporte de
![]() como
Spt
como
Spt![]()
En lo que sigue, utiizaremos la notación y los conceptos introducidos en la sección 3.1.
La variedad afín tórica de un cono poliédrico ![]() se define como
Spec
se define como
Spec![]() .
Mediante la elección adecuada de generadores en
.
Mediante la elección adecuada de generadores en
![]() , la
, la
![]() -álgebra finitamente generada
-álgebra finitamente generada ![]() puede ser representada como un anillo de coordenadas. Tal representación determina, a su vez, una representación de la variedad afín tórica
puede ser representada como un anillo de coordenadas. Tal representación determina, a su vez, una representación de la variedad afín tórica
![]() Spec
Spec![]() . Cualesquiera dos tales representaciones son homeomorfas.
. Cualesquiera dos tales representaciones son homeomorfas.
Sea
![]() un sistema de generadores de
un sistema de generadores de
![]() . Para cada
. Para cada ![]() escribamos
escribamos
![]() . Mediante el isomorfismo
. Mediante el isomorfismo ![]() se obtiene el monomio de Laurent
se obtiene el monomio de Laurent
![]() . La
. La
![]() -álgebra
-álgebra
![]() puede entonces escribirse como
puede entonces escribirse como
![]() para algún ideal
para algún ideal
![]() construido como sigue:
construido como sigue:
Se ve que para cualesquiera
![]() , vale
, vale
![]() en
en
![]() cuando y sólo cuando
cuando y sólo cuando
![]() . Así pues sea
. Así pues sea
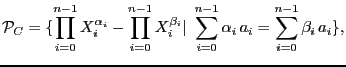
y sea