



Next: Otra representación del toro
Up: Polinomios de Laurent
Previous: Polinomios de Laurent
Contents
Index
Sea 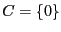 el cono trivial en
el cono trivial en
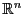 . Entonces el cono dual es
. Entonces el cono dual es
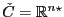 . Para
. Para
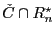 consideremos el conjunto de generadores
consideremos el conjunto de generadores
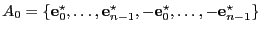 , donde
, donde
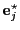 es el
es el  -ésimo vector de la base dual de la canónica en
-ésimo vector de la base dual de la canónica en
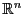 . La correspondiente
. La correspondiente
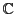 -álgebra monomial es
-álgebra monomial es
donde
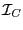 está generado por la familia de polinomios
está generado por la familia de polinomios
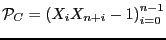 . En consecuencia, la variedad tórica es
Spec
. En consecuencia, la variedad tórica es
Spec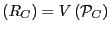 . De hecho la transformación
. De hecho la transformación
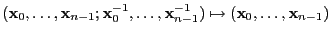 determina un homeomorfismo
Spec
determina un homeomorfismo
Spec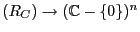 . Como
. Como
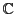 es un campo, se denota
es un campo, se denota
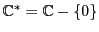 a su grupo multiplicativo. El espacio
a su grupo multiplicativo. El espacio
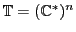 se llama
se llama 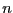 -toro complejo algebraico y es homeomorfo a
-toro complejo algebraico y es homeomorfo a
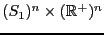 . Por tanto, el
. Por tanto, el 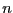 -toro complejo contiene al
-toro complejo contiene al 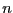 -toro real.
-toro real.
Guillermo Morales-Luna
2011-10-19