


Siguiente: El teorema de Goodstein
Un nivel arriba: Aritmética de Peano
Anterior: Interpretaciones
Veremos aquí que la aritmética de Peano no es completa. Para esto, codificaremos a la aritmética dentro de la misma aritmética y propondremos un enunciado tal que ni él ni su negación son demostrables en AP.
Para cada
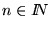 construímos el n-ésimo numeral como
construímos el n-ésimo numeral como
 .
Una relación
.
Una relación
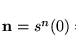 se dice representable en AP si existe una fórmula bien formada
se dice representable en AP si existe una fórmula bien formada
 tal que para cualesquiera
tal que para cualesquiera
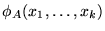 se tiene que rigen las implicaciones
se tiene que rigen las implicaciones
Una función
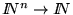 es representable si su gráfica
es representable si su gráfica![[*]](../images/spanish/icons.gif/foot_motif.gif) lo es.
El concepto de demostrabilidad es muy algorítmico, por lo cual una demostración puede verse como un método de cálculo o de comprobación. Así pues, el resultado siguiente aparece de manera muy natural, aunque en este texto omitiremos su demostración.
lo es.
El concepto de demostrabilidad es muy algorítmico, por lo cual una demostración puede verse como un método de cálculo o de comprobación. Así pues, el resultado siguiente aparece de manera muy natural, aunque en este texto omitiremos su demostración.
Teorema 4.1 (Gödel)
Una función es representable si y sólo si es recursiva. Una relación es representable si y sólo si es recursiva.
Ahora, es evidente que el conjunto de fórmulas bien formadas es efectivamente numerable, y cualquiera de los métodos ya vistos de enumeración basta para corroborar esta afirmación. De manera alternativa, sin embargo, podríamos introducir la enumeración g que se muestra en la tabla 5.7. Ahí observamos que los símbolos del alfabeto quedan codificados por números impares, todas las cadenas por números pares divisibles por una potencia impar de 2 y todas las cadenas de cadenas por números pares divisibles por una potencia par de 2.
Table 5.7:
Enumeración de Gödel.
![\begin{table}\begin{center}\fbox{\begin{minipage}[t]{30em}
\begin{displaymath}\...
... es el $k$ -\'esimo n\'umero primo.)
\end{minipage}}\end{center}
\end{table}](img1272.gif) |
Definamos las siguientes relaciones en 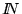 :
:
- 1.
-
 (Fórmula bien formada):
(Fórmula bien formada):
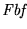
- 2.
-
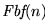 (Axioma lógico):
(Axioma lógico):
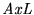
- 3.
-
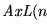 (Axioma propio):
(Axioma propio):

- 4.
-
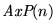 (Demostración):
(Demostración):
- 5.
-
 (Demostrable):
(Demostrable):
- 6.
-
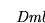 (Sustitución):
(Sustitución):
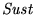
- 7.
-
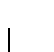 (Instanciación):
(Instanciación):

- 8.
-
 (Cúmplese):
(Cúmplese):
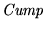
Proposición 4.1
Las relaciones anteriores son todas recursivas y por ende son representables en AP.
Utilizaremos los mismos nombres para denotar a los predicados que representan a esas relaciones. Tenemos entonces que para cualesquiera
 se cumplen las equivalencias siguientes:
se cumplen las equivalencias siguientes:
Hagamos
y sean
 y
y
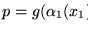 .
Se ve pues que
.
Se ve pues que 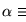 asegura que ningún enunciado de la forma
asegura que ningún enunciado de la forma
 es demostrable, en particular, para
es demostrable, en particular, para
 ,
asevera que
,
asevera que
 no es demostrable, es decir, que
no es demostrable, es decir, que 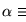 mismo no es demostrable. En otras palabras
mismo no es demostrable. En otras palabras 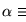 es un enunciado que se refiere a sí mismo y asevera su propia indemostrabilidad.
De aquí resulta que si AP fuese consistente, entonces
es un enunciado que se refiere a sí mismo y asevera su propia indemostrabilidad.
De aquí resulta que si AP fuese consistente, entonces
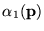 .
Una teoría T, que posea un modelo que incluya a
.
Una teoría T, que posea un modelo que incluya a 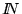 ,
es consistente-
,
es consistente-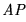 si para cualquier fórmula
si para cualquier fórmula 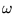 ,
dado que para cada
,
dado que para cada
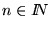 se tuviera que
se tuviera que
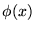 entonces necesariamente
entonces necesariamente
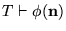 .
Se observa que si T es consistente-
.
Se observa que si T es consistente-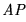 entonces es también consistente, a secas.
Si AP fuese consistente-
entonces es también consistente, a secas.
Si AP fuese consistente-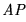 ,
entonces
,
entonces
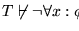 .
Con todo esto se tiene el
.
Con todo esto se tiene el
Teorema 4.2 (Primero de Incompletitud de Gödel)
Si AP fuese consistente-
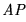
entonces ha de ser incompleta.
Vemos muchas semejanzas entre este teorema de incompletitud y el problema de la parada de máquinas de Turing. En última instancia, las imposibilidades aseveradas por ellos se demuestran utilizando mecanismos autoreferentes. Por otro lado, la capacidad de construir esos mecanismos se debe a sus propios niveles de expresividad y a sus características procedimentales.
Concluímos esta sección presentando el
Teorema 4.3 (Segundo de Incompletitud de Gödel)
En AP no puede demostrarse su propia consistencia.
De manera muy resumida, tenemos los hechos siguientes:
- 1.
- Si H es un conjunto inconsistente de fórmulas bien formadas entonces la teoría de H,
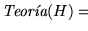 ,
coincide con el conjunto de todas las fórmulas bien formadas. En otras palabras, en una teoría inconsistente cualquier cosa es demostrable.
,
coincide con el conjunto de todas las fórmulas bien formadas. En otras palabras, en una teoría inconsistente cualquier cosa es demostrable.
- 2.
- Un enunciado
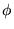 ,
con número de Gödel
,
con número de Gödel  ,
es demostrable en AP si y sólo si
,
es demostrable en AP si y sólo si
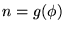 y es indemostrable en AP si y sólo si
y es indemostrable en AP si y sólo si
 .
.
- 3.
- En AP se puede mostrar que 0 es distinto a 1=s(0). La negación de esta desigualdad es
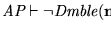 .
Así pues, tendremos que AP es consistente si y sólo si no se puede demostrar
.
Así pues, tendremos que AP es consistente si y sólo si no se puede demostrar  .
Sea pues
.
Sea pues
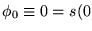 y sea
y sea
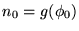 .
El Segundo Teorema de Incompletitud de Gödel equivale a mostrar queen efecto
.
El Segundo Teorema de Incompletitud de Gödel equivale a mostrar queen efecto
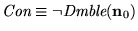 ,
donde
,
donde
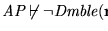 .
.
- 4.
- De acuerdo con la regla modus ponens, si
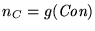 ,
,
 y
y
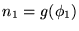 entonces
entonces
- 5.
- Además tenemos que todo lo demostrable es demostrablemente demostrable, es decir, si
 y
y
 entonces
entonces
- 6.
- Por todo lo anterior, para probar el Segundo Teorema de Incompletitud basta ver que
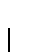 es demostrablemente equivalente en AP al enunciado
es demostrablemente equivalente en AP al enunciado 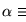 demostrado indemostrable en el Primer Teorema de Incompletitud.
Utilicemos la notación
demostrado indemostrable en el Primer Teorema de Incompletitud.
Utilicemos la notación
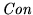 para denotar a la fórmula
para denotar a la fórmula
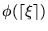 donde
donde 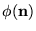 .
Esquemáticamente tenemos:
Veamos primero
.
Esquemáticamente tenemos:
Veamos primero
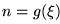 :
:
pues
 .
Recíprocamente, veamos
.
Recíprocamente, veamos
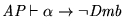 :
:



Siguiente: El teorema de Goodstein
Un nivel arriba: Aritmética de Peano
Anterior: Interpretaciones
Guillermo Morales-Luna
2000-07-10
 .
Una relación
.
Una relación
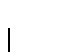 (Demostrable):
(Demostrable):
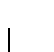 (Instanciación):
(Instanciación):
 entonces
entonces
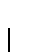 es demostrablemente equivalente en AP al enunciado
es demostrablemente equivalente en AP al enunciado