



Siguiente: Partición
Un nivel arriba: Atercetamientos
Anterior: Atercetamientos
Este problema, llamado en inglés 3-dimensional matching, se formaliza como sigue,
Instancia:
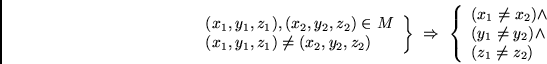
Solución:

Naturalmente, más que planteado como un problema de decisión 3DM se plantea como uno de solución. Así que en caso de que hubiera un tal atercetamiento, habría que localizarlo explícitamente.
Proposición: 3DM es completo-NP.
Demostración: Que este problema esté en NP es fácil de ver:
- 1.
- Se conjetura un posible atercetamiento M' incluído en M, con n tercetas.
- 2.
- Se revisa que cada una de las proyecciones cubra a los conjuntos ``coordenadas''.
Para probar que es difícil-NP, veamos que 3SAT se reduce a 3DM.
Dados
-
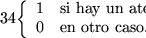 :
conjunto de n variables proposicionales,
:
conjunto de n variables proposicionales,
-
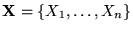 :
conjunto de m cláusulas de 3 literales sobre
:
conjunto de m cláusulas de 3 literales sobre
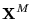 ,
,
construiremos una instancia de 3DM de manera que ésta dé una instancia con respuesta positiva en 3DM si y sólo si la forma conjuntiva
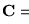 es satisfactible. En tal caso, un atercetamiento en la instancia construída ha de determinar una asignación de valores de verdad a las variables en
es satisfactible. En tal caso, un atercetamiento en la instancia construída ha de determinar una asignación de valores de verdad a las variables en
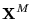 que satisfaga a
que satisfaga a
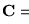 .
Definamos
.
Definamos
-
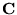 :
Tiene 2nm elementos.
:
Tiene 2nm elementos.
-
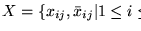 donde
donde
-
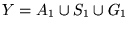 :
Tiene nm elementos.
:
Tiene nm elementos.
-
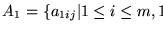 :
Tiene m elementos.
:
Tiene m elementos.
-
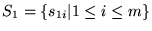 :
Tiene m(n-1) elementos.
:
Tiene m(n-1) elementos.
-
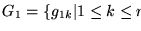 donde
donde
-
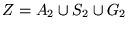 :
Tiene nm elementos.
:
Tiene nm elementos.
-
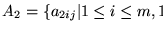 :
Tiene m elementos.
:
Tiene m elementos.
-
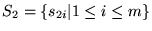 :
Tiene m(n-1) elementos.
:
Tiene m(n-1) elementos.
Consecuentemente, tanto Y como Z poseen 2nm elementos cada uno.
- Tercetas de asignación: Para cada variable Xj construímos los conjuntos de tercetas
El propósito de esta definición es que todo atercetamiento M' con 2nm tercetas debe satisfacer las condiciones siguientes:
así pues, un tal atercetamiento fuerza de manera natural un valor de verdad en la variable Xj.
- Tercetas de satisfacción: Para cada cláusula ci construímos el conjunto
- Tercetas de relleno: Construímos el conjunto
- Instancia para 3DM:
Consecuentemente,

Soluciones de 3SAT corresponden a soluciones de 3DM: Supongamos que la asignación
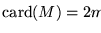 satisface a la forma conjuntiva C. Consideremos las siguientes tercetas:
Se tiene que
satisface a la forma conjuntiva C. Consideremos las siguientes tercetas:
Se tiene que
es un atercetamiento de 2nm tercetas incluído en la instancia M.
Soluciones de 3DM corresponden a soluciones de 3SAT: Sea M' un atercetamiento en M con 2nm elementos. Por la construcción de las tercetas, necesariamente
- A lo más (n-1)m tercetas de M' son del tipo M3,
- a lo más m tercetas de M' son del tipo M2, y
- a lo más nm tercetas de M' son del tipo M1.
Puesto que M' contiene 2nm tercetas las anteriores cotas se alcanzan efectivamente.
Las del tipo M1 son de la forma
donde
![$J_0\cup J_1=[1,n]$](img1766.gif) .
Pues bien la asignación
.
Pues bien la asignación
satisface a la instancia de 3SAT. En cada cláusula la literal que se satisface es la que aparece en la correspondiente terceta del tipo M2 en M'.




Siguiente: Partición
Un nivel arriba: Atercetamientos
Anterior: Atercetamientos
Guillermo Morales-Luna
2000-07-10
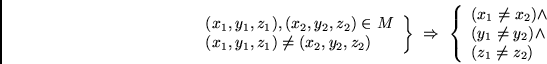

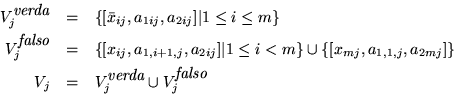
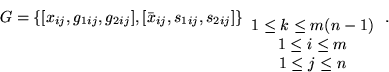
![$J_0\cup J_1=[1,n]$](img1766.gif) .
Pues bien la asignación
.
Pues bien la asignación