



Siguiente: Esquema de recursión
Un nivel arriba: Propiedades de cerradura de
Anterior: Esquema de minimización
La única diferencia, que efectivamente es muy sustancial, con el esquema de minimización es que dada una función
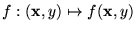 de n+1 argumentos al construir su minimización
de n+1 argumentos al construir su minimización
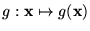 asociándole a cada
asociándole a cada
 el mínimo y para el cual se anula la sección
el mínimo y para el cual se anula la sección
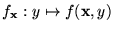 ,
para cada
,
para cada
 se busca la y correspondiente hasta que no se exceda un cierto límite z marcado por un (n+1)-ésimo argumento para g. Así pues, este esquema toma una función de n+1 argumentos y produce otra de n+1 argumentos,
Si
se busca la y correspondiente hasta que no se exceda un cierto límite z marcado por un (n+1)-ésimo argumento para g. Así pues, este esquema toma una función de n+1 argumentos y produce otra de n+1 argumentos,
Si
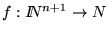 es una función definimos
es una función definimos
Observamos que si
![$\mu_{y\leq z} {[f=0]}(\mbox{\bf x},z)=z$](img245.gif) entonces pueden ocurrir dos situaciones: Bien
entonces pueden ocurrir dos situaciones: Bien
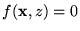 o bien ningún
o bien ningún 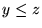 cumple que
cumple que
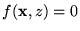 .
Cuál de estos dos casos ocurre puede dilucidarse calculando el valor de
.
Cuál de estos dos casos ocurre puede dilucidarse calculando el valor de
![$\mu_{y\leq z+1} {[f=0]}(\mbox{\bf x},z+1)$](img248.gif) .
Así pues,
.
Así pues,
![$\mbox{\it MiAc}(f)=(\mu_{y\leq z}{[f=0]}).$](img249.gif)
Guillermo Morales-Luna
2000-07-10
![\begin{eqnarray*}(\mu_{y\leq z} {[f=0]}):I\!\!N^n\times I\!\!N&\rightarrow& I\!\...
...tal $y$ ,} \\
z &\mbox{\rm en otro caso.}
\end{array}\right.
\end{eqnarray*}](img244.gif)