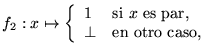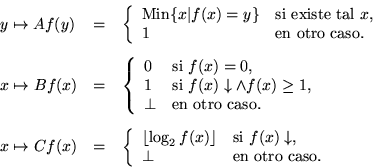Siguiente: Primera lista de programas
Un nivel arriba: Conceptos básicos
Anterior: Observaciones sobre la codificación
1. Pruebe que no existen dos enteros p,q tales que
 .
.
2. Demuestre que si
 es tal que abx=xab entonces existe n tal que x=(ab)n.
es tal que abx=xab entonces existe n tal que x=(ab)n.
3. Encuentre la falacia de la siguiente ``prueba'' de que cualesquiera dos números 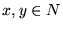 son iguales.
Sea
son iguales.
Sea
Evidentemente P(0) es verdadera.
Ahora, suponga que se cumple P(n). Veamos que se ha de cumplir P(n+1). Si
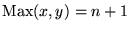 entonces
entonces
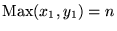 ,
donde x1=x-1 y y1=y-1. Por la hipótesis de inducción se ha de tener x1=y1. Luego x=y, por lo que P(n+1) es cierto.
,
donde x1=x-1 y y1=y-1. Por la hipótesis de inducción se ha de tener x1=y1. Luego x=y, por lo que P(n+1) es cierto.
4. Encuentre la falacia de la siguiente ``prueba'' de que
Demostración: Sea
Probemos por inducción en
 que cualesquiera dos elementos en GN son de un mismo color.
Si n=1 la aseveración es correcta.
Supongamos que hay n+1 gatos. Quitemos uno, que llamamos Yago. Los restantes son n y por la hipótesis de inducción son todos del mismo color. Devolvemos a Yago y quitamos otro, digamos Prudence. Quedan n y por tanto todos ellos son del mismo color. Yago y Prudence han de ser del mismo color y consecuentemente todos los gatos son del mismo color.
que cualesquiera dos elementos en GN son de un mismo color.
Si n=1 la aseveración es correcta.
Supongamos que hay n+1 gatos. Quitemos uno, que llamamos Yago. Los restantes son n y por la hipótesis de inducción son todos del mismo color. Devolvemos a Yago y quitamos otro, digamos Prudence. Quedan n y por tanto todos ellos son del mismo color. Yago y Prudence han de ser del mismo color y consecuentemente todos los gatos son del mismo color.
5. Estime el número de bits necesarios para almacenar el código de Cantor de una sucesión de m números enteros, cada uno de los cuales se escribe con a lo sumo n bits.
6. Decida cuáles de los siguientes conjuntos son numerables. Justifique su respuesta:
a) El conjunto de máquinas de Turing.
b) El conjunto de números complejos.
c) El conjunto de números racionales.
d) El conjunto de intervalos en los reales, abiertos o cerrados, con extremos racionales.
e) El conjunto de funciones INYECTIVAS de N en N.
f) El conjunto de polinomios con coeficientes racionales.
h) El conjunto de programas en C.
7. Un programa-while sin instrucciones while se dice ser un programa rectilíneo.
a) Muestre que todo programa-while que posee exactamente una variable es equivalente a un programa rectilíneo, en el sentido de que ambos calculan a la misma función.
b) Muestre que toda función calculada por un programa rectilíneo es total.
c) Construya un programa-while con exactamente dos variables que no sea equivalente a programa rectilíneo alguno.
Sugerencia: Utilice lo mostrado en el inciso b).
8. Escriba programas-while 's para calcular cada una de las siguientes funciones:
9. Escriba un programa-while que calcule a la función z:=x- en términos de las funciones z:=0 y z:=x++.
10. Muestre que se obtiene exactamente a la misma clase de programas-while 's si sustituímos las pruebas de la forma 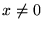 por las de la forma
por las de la forma  .
.
11. Muestre que ningún programa-while de una sola variable puede calcular a la función
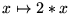 .
.
12. Clasifique a las funciones
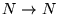 que se calculan por
a) los programas rectilíneos de una sola variable.
b) los programas rectilíneos con cualquier número de variables.
que se calculan por
a) los programas rectilíneos de una sola variable.
b) los programas rectilíneos con cualquier número de variables.
13. a) Muestre que la función
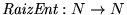 tal que
tal que
 es computable.
b) Muestre que el exceso de cuadrado
es computable.
b) Muestre que el exceso de cuadrado
![$\mbox{\it ExCua}:x\mapsto x\stackrel{\cdot}{-}\left[\mbox{\it RaizEnt}(x)\right]^2$](img314.gif) es computable.
es computable.
14. Muestre que las siguientes funciones son computables:
a)
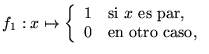 b)
b)
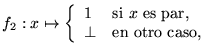
15. a) Muestre que las funciones computables son computables, también, por máquinas de Turing.
b) Muestre que las funciones computables por máquinas de Turing son, también, computables por programas-while 's.
16. Muestre que las siguientes funciones son computables
17. Muestre que si
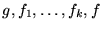 son funciones computables, entonces las funciones
son funciones computables, entonces las funciones
 y
y
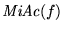 son computables también.
son computables también.
18. Muestre que si g,h,c son computables, entonces las funciones
 y
y
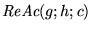 son computables también.
son computables también.
19. Muestre que si en el esquema de minización se omite la exigencia de que la función f sobre la que se aplica sea total entonces habría funciones computables cuya minimización no lo sería.
20. Para una función
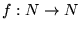 definamos las funciones siguientes:
definamos las funciones siguientes:
a) Muestre que la clase de funciones computables de un solo argumento son cerradas bajo los operadores B y C.
b) Muestre que la clase de funciones computables de un solo argumento que además son crecientes y tienen una imagen infinita son cerradas bajo A pero no bajo B y C.




Siguiente: Primera lista de programas
Un nivel arriba: Conceptos básicos
Anterior: Observaciones sobre la codificación
Guillermo Morales-Luna
2000-07-10
 .
.

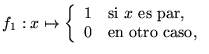 b)
b)