Siguiente: Lenguajes formales de programación Un nivel arriba: Conceptos básicos Anterior: Inducción recurrente

Enumeración de Cantor

A finales del siglo pasado y principios de éste el matemático alemán Georg Cantor (1845-1918) estableció las bases de los números tranfinitos. El primer numeral infinito, denotado por $\omega_0$, puede ser identificado con la cardinalidad de los números naturales. En el estudio de las cardinalidades es importante reconocer como equipotentes, es decir ``con la misma cardinalidad'', a cualesquiera dos conjuntos que, en efecto, lo sean. Una gran constribución de Cantor es su análisis de los conjuntos numerables. Consideremos la función $c:I\!\!N^2\rightarrow I\!\!N$, $c:(x,y)\mapsto \frac{1}{2}(x+y)(x+y+1)+x$. En la tabla (1.1) presentamos como una matriz (infinita) los valores de esta función. En la entrada correspondiente al renglón y y a la columna x presentamos el valor c(x,y). Obsérvese que los valores de c son consecutivos a lo largo de cada diagonal x+y=d, $d\in I\!\!N$. Obsérvese también que c está dado por un polinomio cuadrático.

  

Table 1.1: Función diagonal de Cantor.

De los valores mostrados en la Tabla 1 se puede tener una idea muy precisa de la enumeración que hace c de $I\!\!N^2$. Resulta evidente que cada entrada de la tabla tiene asociado un número natural y, viceversa, cada número natural estará en correspondencia con alguna entrada en la tabla. c es pues una biyección, es decir, es una función inyectiva y suprayectiva. c se dice ser la enumeración de Cantor. Así pues, $I\!\!N^2$ es numerable, es decir, de la misma cardinalidad que $I\!\!N$. A partir de esto es fácil ver por inducción que $\forall n>0, I\!\!N^n$ es también numerable. De hecho, la enumeración de Cantor da procedimientos para enumerar a cada potencia $I\!\!N^n$. En efecto, reiterando la enumeración de Cantor, hagamos

$$\begin{eqnarray*}&& f_1:x\mapsto x \\ \forall n\geq 0&:& f_{n+1}:(\mbox{\bf x}... ...mbox{\bf x})-1,f_{\mbox{\rm Long}(\mbox{\bf x})}(\mbox{\bf x})) \end{eqnarray*}$$

Es fácil ver también que la función $f^*:I\!\!N^*=\bigcup_{n\geq 0}I\!\!N^n \rightarrow I\!\!N$ es una biyección. Para cada secuencia de números naturales $\mbox{\bf x}\in I\!\!N^*$ el número $\lceil\mbox{\bf x}\rceil=f^*(\mbox{\bf x})$ se dice ser el código de la secuencia $\mbox{\bf x}$. Recíprocamente, dado un número $n\in I\!\!N$ la secuencia $\mbox{\bf x}\in I\!\!N^*$ tal que $\lceil\mbox{\bf x}\rceil=n$ es la secuencia codificada por n y, en tal caso, escribimos $\mbox{\bf x}=\lfloor n\rfloor$. En la tabla (1.2) se ejemplifica la relación entre secuencias y códigos.

  

Table: Valores de $f^*(\{1,\ldots,i\})$ para $i=1,\ldots,10$.

En la tabla (1.3) se ejemplifica la relación inversa entre códigos y secuencias.

  

Table: Valores de (f^*)^-1(n) para $n=1953,\ldots,1960$.

Resumiendo, tenemos la

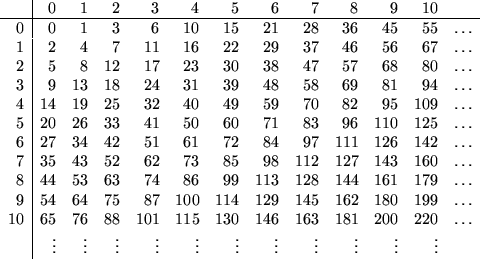
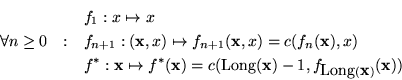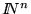
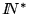
Proposición 3.1   Para cada n>0 la potencia cartesiana $I\!\!N^n$ es numerable, y lo es también el conjunto $I\!\!N^*$ consistente de las secuencias de números naturales. Más aún cada uno de estos conjuntos posee una enumeración efectivamente calculable con inversa también efectivamente calculable.

$I\!\!N^2$ es enumerable mediante la enumeración c que está dada por un polinomio. Por lo cual es efectivamente calculable. En la figura (1.1) mostramos un seudocódigo, que se explica por sí mismo, para calcular a la función f_n.

  

Figure 1.1: Cálculo de la función f_n.

En la figura (1.2) mostramos un seudocódigo para calcular a la función f^*.

  

Figure 1.2: Cálculo de la función f_n.

En la figura (1.3) mostramos un seudocódigo para calcular a la inversa de la enumeración c.

  

Figure 1.3: Cálculo de la inversa de c.

En la figura (1.4) mostramos un seudocódigo recursivo en n para calcular a la inversa de cada una de las funciones f_n.

  

Figure 1.4: Cálculo de la inversa de f_n.

Finalmente, en la figura (1.5) mostramos un seudocódigo para calcular a la inversa de la función f^*.

  

Figure 1.5: Cálculo de la inversa de f^*.

Siguiente: Lenguajes formales de programación Un nivel arriba: Conceptos básicos Anterior: Inducción recurrente