Siguiente: Función de Gödel Un nivel arriba: Función de Gödel Anterior: Algoritmo de Euclides

Teorema chino del residuo

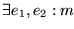
Teorema 3.1   Si (m,n)=1 entonces, cualesquiera que sean los números $r,s\in Z\!\!\!Z$ el sistema de ecuaciones

$$\begin{eqnarray*}x &\equiv& r\mbox{\rm mod }m \\ x &\equiv& s\mbox{\rm mod }n \end{eqnarray*}$$

posee una solución x₀. De hecho todo entero congruente con x₀ módulo mn es también una solución.

Demostración: Sean a,b tales que am-bn=1. Multiplicando por (r-s) tenemos

r-s=a(r-s)m-b(r-s)n.

Así que

r-a(r-s)m=s-b(r-s)n.

Denotemos por x₀ a ese valor común. Se tiene que x₀ es una solución del sistema de ecuaciones.


Iterando este resultado, obtenemos el siguiente

Teorema 3.2   Sea $\left[n_i\right]_{i=1,\ldots,k}$ una sucesión finita de enteros positivos, primos relativos a pares:

$$i_1\not=i_2\;\Rightarrow\;(n_{i_1},n_{i_2})=1.$$

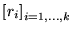
Sea $\left[r_i\right]_{i=1,\ldots,k}$ una sucesión, de igual longitud, de enteros arbitrarios. Entonces existe una solución $x_0^k\in Z\!\!\!Z$ del sistema de ecuaciones

$$x\equiv r_i\mbox{\rm mod }n_i,\ i=1,\ldots,k.$$

De hecho x₀^k se calcula recursivamente: Si x₀^k-1 es una solución de las primeras (k-1) ecuaciones entonces x₀^k es una solución del sistema de ecuaciones

$$\begin{eqnarray*}x &\equiv& x_0^{k-1}\mbox{\rm mod }\left(\prod_{i=1}^{k-1}n_i\right) \\ x &\equiv& r_k\mbox{\rm mod }n_k \end{eqnarray*}$$

Ejemplos. Supongamos que $\mbox{\bf r}$ es la sucesión de los primeros diez enteros positivos y que $\mbox{\bf n}$ es la sucesión de los primeros diez números primos:

$$\begin{eqnarray*}\mbox{\bf r} &=& [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]^T \\ \mbox{\bf n} &=& [2, 3, 5, 7, 11, 13, 17, 19, 23, 29]^T \end{eqnarray*}$$

Procediendo recursivamente para calcular una solución del sistema de ecuaciones

$$x\mbox{\bf 1}\equiv \mbox{\bf r}\mbox{\rm mod }\mbox{\bf n}\h... ... }\left[\begin{array}{c} n_1 \\ \vdots \\ n_k\end{array}\right]$$

obtenemos sucesivamente los valores mostrados en la tabla 3.4.

  

Table 3.4: Ejemplo del Teorema Chino del Residuo.

Así pues toda solución del sistema de ecuaciones es de la forma

$$x\equiv 5765999453\mbox{\rm mod } 6469693230.$$

Siguiente: Función de Gödel Un nivel arriba: Función de Gödel Anterior: Algoritmo de Euclides