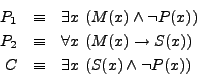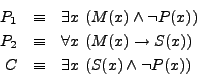

Next: Camenes
Up: Silogística
Previous: Festino
Para demostrar la validez de este silogismo, escribamos:
Ya que 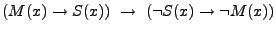 es un teorema,
resulta
es un teorema,
resulta 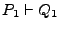 , en donde
, en donde 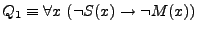 . Hagamos
. Hagamos 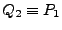 . Por Festino resulta
. Por Festino resulta 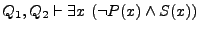 , es decir
, es decir 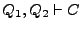 . Consecuentemente se tiene
. Consecuentemente se tiene 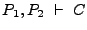 .
. 

Guillermo Morales-Luna
2007-04-24