next up previous
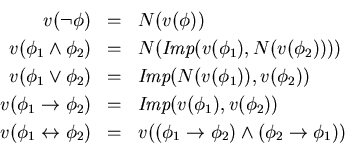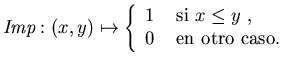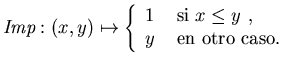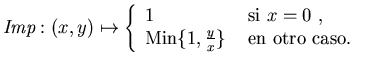
Siguiente: Problemas típicos de lógicas Un nivel arriba: Lógicas proposicionales difusas Anterior: Semánticas basadas en conjunción

Semánticas basadas en implicación y negación

Hasta ahora hemos extendido los conectivos siguiendo principalmente dos enfoques: En uno consideramos una conjunción y una negación como básicos. En otro, consideramos una conjunción, en términos de ella definimos una implicación, y estos dos conectivos fueron considerados para ser los básicos.

Para finalizar las posibles extensiones de asignaciones, supongamos dadas una implicación $\mbox{\it Imp}:[0,1]^2\rightarrow[0,1]$ y una negación $N:[0,1]\rightarrow[0,1]$ como conectivos básicos. Entonces podemos extender valores de verdad a los demás conectivos como sigue:

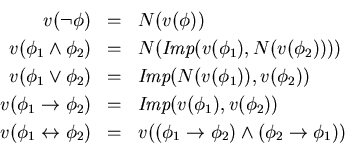
\begin{eqnarray*}v(\neg \phi) &=& N(v(\phi)) \\ v(\phi_1\land \phi_2) &=& N(\m... ...&=& v((\phi_1\rightarrow \phi_2)\land(\phi_2\rightarrow \phi_1)) \end{eqnarray*}


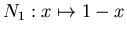Veamos algunos ejemplos. En todos ellos supondremos que la negación es $N_1: x\mapsto 1-x$.

Producto-D.
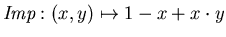Para la función $\mbox{\it Imp}:(x,y)\mapsto 1-x+x\cdot y$ obtenemos los mismos operadores que en el caso Producto-D definido anteriormente.
\Lukasiewicz-D.
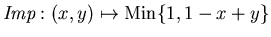Para la función $\mbox{\it Imp}:(x,y)\mapsto \mathop{\rm Min}\{1,1-x+ y\}$ obtenemos los mismos operadores que en el caso \Lukasiewicz-D definido anteriormente.
Implicación por inclusión.
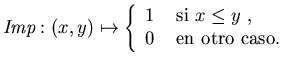
Consideremos $\mbox{\it Imp}:(x,y)\mapsto \left\{\begin{array}{ll} 1 &\mbox{ si $x\leq y$ , } \\ 0 &\mbox{ en otro caso. } \end{array}\right.$

Se tiene que los conectivos tendrán las funciones mostradas en el recuadro (14).

  
Table 14: Conectivos resultantes de la implicación por inclusión.
\begin{table}\begin{center}\fbox{\begin{minipage}[t]{30em} \begin{eqnarray*} v(... .... } \end{array}\right. % \end{eqnarray*}\end{minipage}}\end{center} \end{table}

Implicación de Brower o por falla.
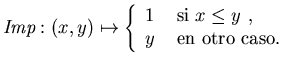
Consideremos $\mbox{\it Imp}:(x,y)\mapsto \left\{\begin{array}{ll} 1 &\mbox{ si $x\leq y$ , } \\ y &\mbox{ en otro caso. } \end{array}\right.$

Se tiene que los conectivos tendrán las funciones mostradas en el recuadro (15).

  
Table 15: Conectivos resultantes de la implicación de Brower.
\begin{table}\begin{center}\fbox{\begin{minipage}[t]{30em} \begin{eqnarray*} v(... ...ot=0 . \end{array}\right. \end{eqnarray*}\end{minipage}}\end{center} \end{table}

En este caso, ni la conjunción ni la disyunción son conmutativas.
Implicación de Zadeh.
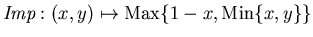
Consideremos $\mbox{\it Imp}:(x,y)\mapsto \mathop{\rm Max}\{1-x,\mathop{\rm Min}\{x,y\}\}$

Se tiene que los conectivos tendrán las funciones mostradas en el recuadro (16).

  
Table 16: Conectivos resultantes de la implicación de Zadeh.
\begin{table}\begin{center}\fbox{\begin{minipage}[t]{33em} \begin{eqnarray*} v(... ...)> 1]. \end{array}\right. \end{eqnarray*}\end{minipage}}\end{center} \end{table}

En este caso, ni la conjunción ni la disyunción son conmutativas.
Implicación de Bayes.
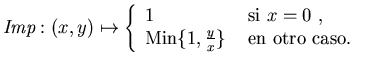
Consideremos $\mbox{\it Imp}:(x,y)\mapsto \left\{\begin{array}{ll} 1 &\mbox{ si $x=0$ , } \\ \mathop{\rm Min}\{1,\frac{y}{x}\} &\mbox{ en otro caso. } \end{array}\right.$

Se tiene que los conectivos tendrán las funciones mostradas en el recuadro (17).

  
Table 17: Conectivos resultantes de la implicación de Bayes.
\begin{table}\begin{center}\fbox{\begin{minipage}[t]{30em} \begin{eqnarray*} v(... ...hi_2). \end{array}\right. \end{eqnarray*}\end{minipage}}\end{center} \end{table}

En este caso, ni la conjunción ni la disyunción son conmutativas.

next up previous
Siguiente: Problemas típicos de lógicas Un nivel arriba: Lógicas proposicionales difusas Anterior: Semánticas basadas en conjunción
Guillermo Morales-Luna
2000-03-14